Trả lời bởi giáo viên
Đáp án đúng: b
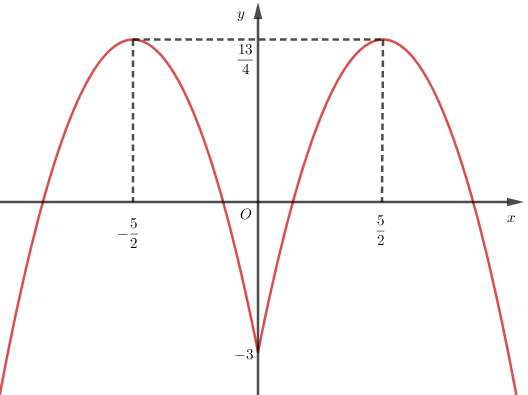
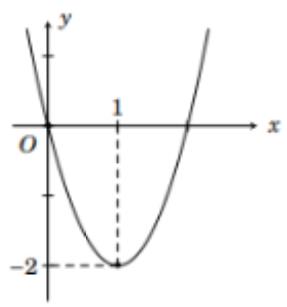
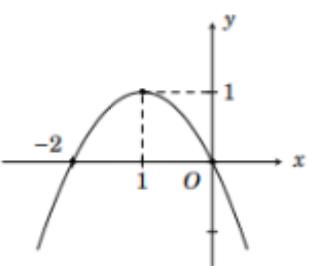
Quan sát đồ thị ta loại A. và D.
Phần đồ thị bên phải trục tung là phần đồ thị \(\left( P \right)\) của hàm số bậc hai, tọa độ đỉnh của \(\left( P \right)\) là \(\left( {\dfrac{5}{2};\dfrac{{13}}{4}} \right)\), trục đối xứng là \(x = \dfrac{5}{2}\), đi qua điểm \(\left( {0; - 3} \right)\)
Ta có: \(\left( {0;3} \right) \in \left( P \right) \Rightarrow c = - 3\)
Trục đối xứng \(x = \dfrac{5}{2}\) \( \Rightarrow - \dfrac{b}{{2a}} = \dfrac{5}{2} \Leftrightarrow b = - 5a \)
Do đó ta có phương trình \(y = a{x^2} - 5ax - 3\)
Đỉnh \(\left( {\dfrac{5}{2};\dfrac{{13}}{4}} \right)\) nên \(\dfrac{{13}}{4} = a.\dfrac{{25}}{4} - a.\dfrac{{25}}{2} - 3 \Leftrightarrow a = - 1\)
Vậy phần đồ thị bên phải là một phần của parabol \(\left( P \right):y = - {x^2} + 5x - 3\)
Phần đồ thị bên trái trục tung là do lấy đối xứng phần đồ thị bên phải của $\left( P \right)$qua trục tung $Oy$. Ta được cả hai phần là đồ thị của hàm số $y = - {x^2} + 5\left| x \right| - 3$.
Hướng dẫn giải:
Quan sát dáng đồ thị hàm số, dùng phương pháp loại trừ kết hợp với tìm phương trình parabol ban đầu để suy ra đáp án đúng.
