Câu hỏi:
3 năm trước
Điều kiện của \(m\) để phương trình \(\left| {{x^2} - 2x - 3} \right| = m\) có đúng hai nghiệm phân biệt là
Trả lời bởi giáo viên
Đáp án đúng: c
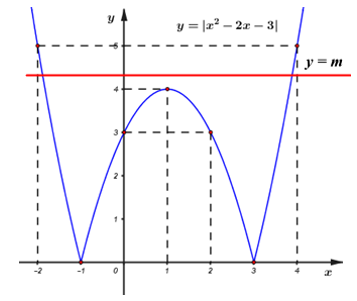
Từ đồ thị hàm số \(y = {x^2} - 2x - 3,\) giữ lại phần đồ thị phía trên trục hoành, lấy đối xứng phần đồ thị phía dưới trục hoành lên phía trên trục hoành ta được đồ thị hàm số \(y = \left| {{x^2} - 2x - 3} \right|.\)
Dựa vào đồ thị ta thấy, \(\left| {{x^2} - 2x - 3} \right| = m\) có đúng 2 nghiệm phân biệt khi và chỉ khi \(\left[ \begin{array}{l}m > 4\\m = 0\end{array} \right.\)
Hướng dẫn giải:
Số nghiệm của phương trình \(\left| {{x^2} - 2x - 3} \right| = m\) chính là số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 2x - 3} \right|\) và đường thẳng \(y = m\).