Câu hỏi:
2 năm trước
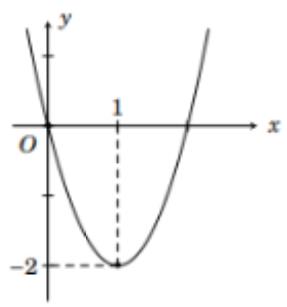
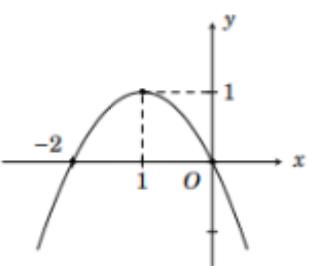
Cho Parabol \(\left( P \right):y = \left| {{x^2} - 3x - 1} \right| + 2\). Tìm \(m\) để đường thẳng \(d:y = - m + 1\) cắt \(\left( P \right)\) tại đúng 3 điểm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: b
Hoành độ giao điểm của (P) và d là nghiệm của phương trình
\(\left| {{x^2} - 3x - 1} \right| + 2 = - m + 1\)\( \Leftrightarrow \left| {{x^2} - 3x - 1} \right| = - m - 1\)
Vẽ đồ thị hàm số \(y = \left| {{x^2} - 3x - 1} \right|\) trên cùng một hệ trục tọa độ:
+) Vẽ parabol \(\left( {{P_1}} \right):{x^2} - 3x - 1\)
+) Vẽ parabol \(\left( {{P_2}} \right): - \left( {{x^2} - 3x - 1} \right)\) bằng cách lấy đối xứng \(\left( {{P_1}} \right)\) qua \(Ox\).
+) Xóa đi phần đồ thị của \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) dưới trục hoành.
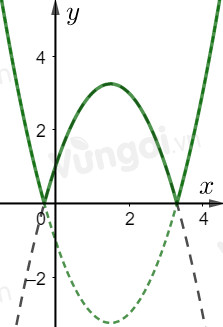
Dựa vào đồ thị ta thấy phương trình đã cho có đúng 3 nghiệm phân biệt khi và chỉ khi \(y = - m - 1\) đi qua đỉnh của \(\left( {{P_2}} \right)\) \( \Leftrightarrow - m - 1 = - \dfrac{{{3^2} - 4.\left( { - 1} \right).1}}{{4.\left( { - 1} \right)}} \Leftrightarrow m = - \dfrac{{17}}{4}\)
Hướng dẫn giải:
Vẽ đồ thị hàm số \(\left( {{P_1}} \right):{x^2} - 3x - 1\) và \(\left( {{P_2}} \right): - \left( {{x^2} - 3x - 1} \right)\) trên cùng một hệ trục tọa độ. Bỏ phần dưới đồ thị ta được đồ thị của \(\left( P \right)\). Dựa vào đồ thị để xác định \(m\).
