Câu hỏi:
2 năm trước
Tìm m để đường thẳng \(\left( d \right):y = \dfrac{{ - 2m - 1}}{3}\) cắt đồ thị của hàm số \(\left( P \right):y = {x^2} - 3\left| x \right| + 1\) tại đúng 2 điểm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: d
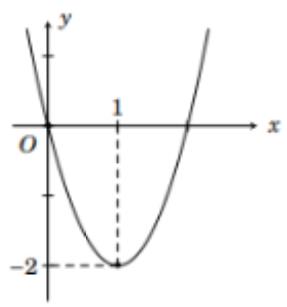
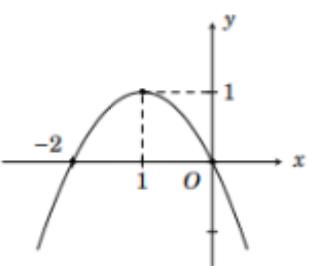
Ta có hàm số (P): \(y = \left\{ \begin{array}{l}{x^2} - 3x + 1{\rm{ khi }}x \ge 0\\{x^2} + 3x + 1{\rm{ khi }}x < 0\end{array} \right.\)
Vẽ đồ thị của hàm số \(\left( P \right):y = {x^2} - 3\left| x \right| + 1\).
- Vẽ Parabol \(({P_1}):y = {x^2} - 3x + 1\). Bỏ đi phần đồ thị bên trái trục tung.
- Vẽ Parabol \(({P_2}):y = {x^2} + 3x + 1\) bằng cách lấy đối xứng \(\left( {{P_1}} \right)\) qua trục \(Oy\).
Ta được đồ thị của \(\left( P \right):y = {x^2} - 3\left| x \right| + 1\) như sau:
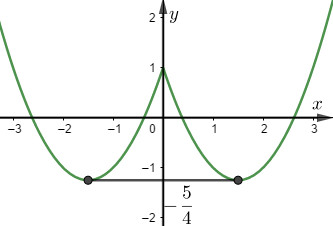
Từ đồ thị ta thấy \(\left( d \right):y = \dfrac{{ - 2m - 1}}{3}\) cắt \(\left( P \right)\) tại đúng 2 điểm phân biệt khi và chỉ khi \(\left[ \begin{array}{l}\dfrac{{ - 2m - 1}}{3} = -\dfrac{5}{4}\\\dfrac{{ - 2m - 1}}{3} > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - \dfrac{11}{8}\\m < - 2\end{array} \right.\)
Hướng dẫn giải:
Sử dụng đồ thị để biện luận theo m.
Vẽ đồ thị hàm số \(y = a{x^2} + b\left| x \right| + c\): Vẽ đồ thị hàm số \(y = a{x^2} + bx + c\) với \(x \ge 0\) rồi lấy đối xứng qua trục Oy.
