Trả lời bởi giáo viên
Dựa vào hình vẽ xác định đây là đồ thị hàm số\(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\)
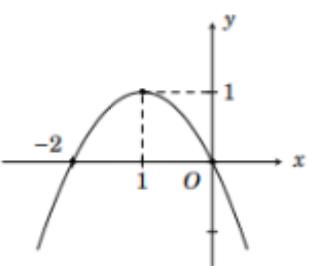
Ta thấy đồ thị hàm số có bề lõm hướng xuống dưới \( \Rightarrow a < 0.\)
Đồ thị có đỉnh \(I\left( { - 1;1} \right) \Rightarrow \left\{ \begin{array}{l}\dfrac{{ - b}}{{2a}} = - 1\\f\left( { - 1} \right) = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\a - b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a - b = 0\\a - b + c = 1\end{array} \right.\,\,\left( 1 \right)\)
Đồ thị hàm số cắt trục hoành tại điểm \(O\left( {0;0} \right) \Rightarrow f\left( 0 \right) = 0 \Leftrightarrow c = 0\)
Thay vào \(\left( 1 \right) \Rightarrow \left\{ \begin{array}{l}2a - b = 0\\a - b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\,\,\left( {tm} \right)\\b = - 2\end{array} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^2} - 2x.\)
Hướng dẫn giải:
Dựa vào dáng điệu của đồ thị hàm số, đỉnh của đồ thị và các điểm mà đồ thị hàm số đi qua để xác định hàm số cần tìm.