Câu hỏi:
2 năm trước
Cho lăng trụ đều \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có \(AB = 2\sqrt 3 ,B{B^\prime } = 2\). Gọi M, N, P tương ứng là trung điểm của \({A^\prime }{B^\prime },{A^\prime }{C^\prime },BC\). Nếu gọi \(\alpha \) là độ lớn góc của hai mặt phẳng \((MNP)\) và \(\left( {AC{C^\prime }} \right)\) thì \(\cos \alpha \) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
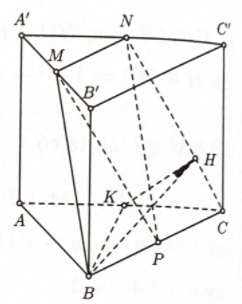
Bước 1: Gọi \(K\) là trung điểm của AC. Chứng minh \(BK \bot NC\)
Gọi \(K\) là trung điểm của A C.
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{BK \bot AC}\\{BK \bot A{A^\prime }}\end{array} \Rightarrow BK \bot \left( {AC{C^\prime }{A^\prime }} \right)} \right.\)\( \Rightarrow BK \bot NC\).
Bước 2: Kẻ \(KH \bot NC(H \in NC)\). Xác định góc giữa \(\left( {MNP} \right)\) và \(\left( {AC{C^\prime }} \right)\)
Kẻ \(KH \bot NC(H \in NC)\), suy ra \(NC \bot (BKH)\)
\( \Rightarrow NC \bot BH\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{(MNP) \cap \left( {ACC'} \right) = NC}\\{BH \bot NC}\\{KH \bot NC}\end{array}} \right.\)
=> Góc giữa \(\left( {MNP} \right)\) và \(\left( {AC{C^\prime }} \right)\) là góc giữa BH và KH và bằng \(\widehat {KHB} = \alpha \)
Bước 3: Tính \(\cos \alpha \)
Do $ABC.A'B'C'$ là lăng trụ đều nên $ABC$ là tam giác đều
=> BK vuông góc với AC
=> BK vuông góc với (ACC'A')
=> BK vuông góc với KH
Hay tam giác BKH vuông tại K.
Lại có \(BK = 3,KH = \dfrac{{2\sqrt {21} }}{7} \Rightarrow BH = \dfrac{{5\sqrt {21} }}{7}\)
Khi đó, \(\cos \alpha = \dfrac{{KH}}{{BH}} = \dfrac{2}{5}\).
Hướng dẫn giải:
Bước 1: Gọi \(K\) là trung điểm của AC. Chứng minh \(BK \bot NC\)
Bước 2: Kẻ \(KH \bot NC(H \in NC)\). Xác định góc giữa \(\left( {MNP} \right)\) và \(\left( {AC{C^\prime }} \right)\)
Bước 3: Tính \(\cos \alpha \)
