Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 3 \), cạnh bên \(AA' = \dfrac{{a\sqrt 6 }}{2}\) (minh họa như hình vẽ).
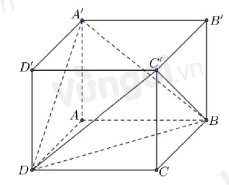
Góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {C'BD} \right)\) bằng bao nhiêu độ?
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
$^o$
Trả lời bởi giáo viên
Đáp án:
$^o$
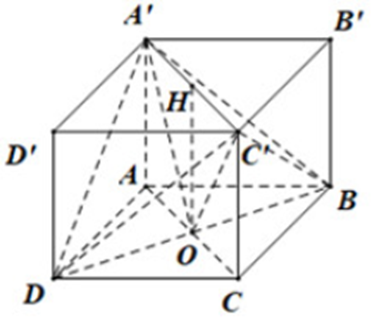
Vì \(ABCD\) là hình vuông nên \(AC \bot BD\) tại \(O\).
Mà \(AC \subset \left( {A'OC'} \right)\) (do \(AC \subset \left( {ACC'A'} \right)\) và \(\left( {A'OC'} \right) \equiv \left( {ACC'A'} \right)\)).
\( \Rightarrow BD \bot \left( {A'OC'} \right)\).
\( \Rightarrow BD \bot A'O\) và \(BD \bot OC'\).
Mà \(A'O \subset \left( {A'BD} \right),\,\,OC' \subset \left( {C'BD} \right)\).
\( \Rightarrow \) Góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {C'BD} \right)\) là \(\widehat {A'OC'}\).
Gọi \(H\) là tâm hình vuông \(A'B'C'D'\). Khi đó \(H\) là trung điểm \(A'C'\).
\( \Rightarrow OH = AA' = \dfrac{{a\sqrt 6 }}{2}\).
Tam giác \(A'C'D'\) vuông tại \(D'\): \(A'{C'^2} = A'{D'^2} + C'{D'^2} = {\left( {a\sqrt 3 } \right)^2} + {\left( {a\sqrt 3 } \right)^2} = 6{a^2}\).
\( \Rightarrow A'C' = a\sqrt 6 \).
\( \Rightarrow A'H = HC' = \dfrac{{A'C'}}{2} = \dfrac{{a\sqrt 6 }}{2}\).
\( \Rightarrow OH = A'H = HC' = \dfrac{{a\sqrt 6 }}{2}\).
\( \Rightarrow \) Tam giác \(A'OC'\) vuông tại \(O\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền).
\( \Rightarrow \widehat {A'OC'} = 90^\circ \).
Vậy góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {C'BD} \right)\) bằng \(90^\circ \).
Hướng dẫn giải:
Bước 1: Xác định góc.
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
Bước 2: Tính độ lớn của góc.

