Bài tập công thức tính nhiệt lượng

Ta có: \(V = 5lit = {5.10^{ - 3}}{m^3}\)

+ Khối lượng nước trong chậu là: \(m = DV = 1000.5.10{}^{ - 3} = 5kg\)

+ Nhiệt lượng nước nhận từ mặt trời để tăng từ \({25^0}C\) lên \({30^0}C\) là:

\(Q = mc\Delta t = 5.4200.\left( {30 - 20} \right) = 105000J = 105kJ\) 

Nhiệt lượng của vật phụ thuộc vào:

     + Khối lượng

     + Độ tăng nhiệt độ của vật

     + Nhiệt dung riêng của chất làm nên vật.

Nhiệt dung riêng của một chất cho biết nhiệt lượng cần truyền cho \(1kg\) chất đó để nhiệt độ tăng thêm \({1^0}C\left( {1K} \right)\)

Đơn vị của nhiệt dung riêng là: \(J/kg.K\)

Ta có: Nhiệt dung riêng của một chất cho biết nhiệt lượng cần truyền cho \(1kg\) chất đó để nhiệt độ tăng thêm \({1^0}C\left( {1K} \right)\)

=> Nhiệt dung riêng của rượu là \(2500J/kg.K\). Điều này có nghĩa là: Để nâng \(1{\rm{ }}kg\) rượu tăng lên \(1\) độ ta cần cung cấp cho nó nhiệt lượng là \(2500{\rm{ }}J\)

Công thức tính nhiệt lượng thu vào:

\(Q = mc\Delta t = mc\left( {{t_2} - {t_1}} \right) = mc\left( {t - {t_0}} \right)\)

A, B, D – đúng

C – sai vì: Độ tăng nhiệt độ của vật càng lớn thì nhiệt lượng mà vật thu vào để nóng lên càng lớn

Ngoài \(J,{\rm{ }}kJ\) đơn vị nhiệt lượng còn được tính bằng \(calo,{\rm{ }}kcalo\)

 \(1kcalo = 1000calo;1{\rm{ }}calo = 4,2J\)

Ta có: Nhiệt lượng : \(Q = mc\Delta t\)

Bình A chứa lượng nước ít nhất (\(1l\)) trong các bình

=> trong cùng một thời gian đun trên bếp cồn như nhau thì nhiệt độ trong bình A là cao nhất

Ta có: Nhiệt dung riêng của một chất cho biết nhiệt lượng cần truyền cho \(1kg\) chất đó để nhiệt độ tăng thêm \({1^0}C\left( {1K} \right)\)

Theo đầu bài, ta có: Nhiệt dung riêng của đồng lớn hơn chì => Để tăng nhiệt độ của \(3kg\) đồng và \(3kg\) chì thêm \({15^0}C\) thì khối đồng sẽ cần nhiều nhiệt lượng hơn khối chì

Ta có \({t_A} < {t_B} < {t_C}\)

=> Ta chỉ có thể chắc chắn rằng: C tỏa nhiệt, A thu nhiệt

Còn B chỉ có thể xác định được tỏa nhiệt hay thu nhiệt sau khi tính được nhiệt độ khi cân bằng

+ Ta có nhiệt độ sôi của nước là \({100^0}C\)

+ Đổi khối lượng của \(15l\) nước \( = 15kg\)

+ Nhiệt lượng cần cung cấp để đun sôi \(15l\) nước từ \({20^0}\) là:

\(Q = mc\Delta t = 15.4200.\left( {100 - 20} \right) = 5040000J = 5040kJ\)

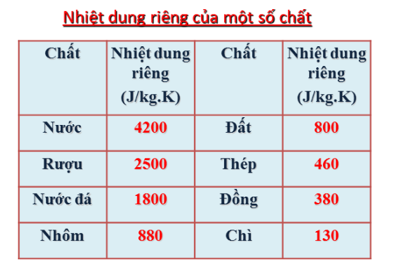
+ Ta có, nhiệt lượng cần cung cấp cho khối lượng kim loại đó là: \(Q = mc\Delta t\)

Ta suy ra, nhiệt dung riêng của kim loại đó là:

\(c = \frac{Q}{{m\Delta t}} = \frac{{110,{{4.10}^3}}}{{8.\left( {70 - 40} \right)}} = 460J/kg.K\)

+ Dựa vào bảng nhiệt dung riêng, ta suy ra kim loại đó là: Thép

+ Đổi đơn vị:

Khối lượng của \(0,5l\) nước \( = 0,5kg = {m_2}\)

Khối lượng của ấm: \({m_1} = 0,3kg\)

Ta có:

+ Nhiệt độ nước sôi là: \({100^0}C\)

+ Nhiệt lượng truyền cho ấm tăng từ \({25^0}C \to {100^0}C\) là: \({Q_1} = {m_1}{c_1}\Delta t\)

+ Nhiệt lượng truyền cho nước sôi từ \({25^0}C \to {100^0}C\) là: \({Q_2} = {m_2}{c_2}\Delta t\)

+ Nhiệt lượng tối thiểu để đun sôi nước trong ấm sẽ bằng tổng nhiệt lượng để truyền cho ấm nóng lên và làm cho nước nóng lên:

\(\begin{array}{l}Q = {Q_1} + {Q_2} = {m_1}{c_1}\Delta t + {m_2}{c_2}\Delta t\\ = 0,3.880\left( {100 - 25} \right) + 0,5.4200\left( {100 - 25} \right)\\ = 177300J = 177,3kJ\end{array}\)

Ta có nhiệt lượng cung cấp: \(Q = mc\Delta t\)

Ta suy ra: \(\Delta t = \frac{Q}{{mc}} = \frac{{{{175.10}^3}}}{{2.2500}} = 35\)

=> Nhiệt độ của rượu tăng thêm là: \({35^0}C\)

+ Đổi đơn vị: Khối lượng của \(15l\) nước \( = 15kg\)

+ Ta có, nhiệt lượng \(Q = mc\Delta t\)

Ta suy ra: \(\Delta t = \dfrac{Q}{{mc}} = \dfrac{{{{1134.10}^3}}}{{15.4200}} = 18\)

Mặt khác, ta có:

\(\begin{array}{l}\Delta t = {t_2} - {t_1} \leftrightarrow 18 = {t_2} - 27\\ \to {t_2} = 18 + 27 = 45\end{array}\)

Vậy nhiệt độ \({t_2}\) có giá trị là \({45^0}C\)

+ Đổi đơn vị: Khối lượng của \(12l\) nước \( = 12kg\)

+ Ta có, nhiệt lượng \(Q = mc\Delta t\)

Ta suy ra: \(\Delta t = \dfrac{Q}{{mc}} = \dfrac{{1562,{{4.10}^3}}}{{12.4200}} = 31\)

Mặt khác, ta có:

\(\begin{array}{l}\Delta t = {t_2} - {t_1} \leftrightarrow 31 = 72 - {t_1}\\ \to {t_1} = 72 - 31 = 41\end{array}\)

Vậy nhiệt độ ban đầu của nước \({t_1}\) có giá trị là \({41^0}C\)

Ta có: \(1calo = 4,2J\)

Nhiệt lượng cần cung cấp cho đồng là: \(Q = mc\Delta t = 10.380.(70 - 20) = 190000J = 190kJ\)

Nhiệt lượng là phần nội năng của vật tăng lên hay giảm đi trong quá trình truyền nhiệt.