Hai chiếc xe ô tô chuyên động trên một đường thẳng có đồ thị đường đi được biểu diễn như hình sau:
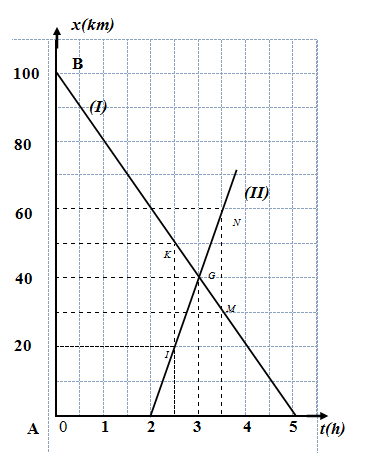
Nhận xét về thời điểm xuất phát của hai xe:
Từ đồ thị, ta thấy hai xe xuất phát từ các thời điểm khác nhau
Xe (I) xuất phát trước xe (II) 2 giờ
Hai chiếc xe ô tô chuyên động trên một đường thẳng có đồ thị đường đi được biểu diễn như hình sau:

Thời điểm và vị trí của hai xe so với điểm A khi chúng gặp nhau.
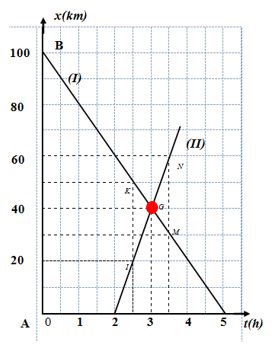
Tọa độ giao điểm của hai đồ thị cho biết:
- Hai xe gặp nhau sau $3h$ kể từ khi xe (I) khởi hành từ $B$, sau $1h$ kể từ khi xe (II) khởi hành từ $A$
- Vị trí gặp cách $A$: $40km$.
Hai chiếc xe ô tô chuyên động trên một đường thẳng có đồ thị đường đi được biểu diễn như hình sau:

Thời điểm của hai xe khi chúng cách nhau 30km
Thời điểm và vị trí hai xe cách nhau $30km$:
Từ thời điểm \(t = 2,5h\) kẻ đường thẳng song song với trục tung cắt hai đồ thị tại hai điểm $I$ và $K$, tung độ của $I$ là \({x_2} = 20km\) , của K là \({x_1} = 50km\).
Vậy hai xe cách nhau \(l = {x_1} - {x_2} = 50 - 20 = 30km\)
Xét tương tự với thời điểm \(t = 3,5h\), ta cũng có hai xe cách nhau \(30km\)
Một người đi xe đạp trên một đoạn đường thẳng AB. Trên \(1/3\) đoạn đường đầu đi với vận tốcc \(14km/h\), \(1/3\) đoạn đường tiếp theo đi với vận tốc \(16km/h\) , \(1/3\) đoạn đường cuối đi với vận tốc \(8km/h\). Vận tốc trung bình của xe đạp trên cả đoạn đường AB có thể nhận giá trị nào? Hãy chọn câu đúng
Gọi thời gian vật đi được trong từng quãng đường lần lượt là: \({t_1},{t_2},{t_3}\)
Ta có: \(\dfrac{{s/3}}{{{v_3}}}\left\{ \begin{array}{l}{t_1} = \dfrac{{{s_1}}}{{{v_1}}} = \dfrac{{s/3}}{{{v_1}}}\\{t_2} = \dfrac{{{s_2}}}{{{v_2}}} = \dfrac{{s/3}}{{{v_2}}}\\{t_3} = \dfrac{{{s_3}}}{{{v_3}}} = \dfrac{{s/3}}{{{v_3}}}\end{array} \right.\)
Vận tốc của ô tô trên cả đoạn đường:
\({v_{tb}} = \dfrac{{{s_1} + {s_2} + {s_3}}}{{{t_1} + {t_2} + {t_3}}} = \dfrac{{s/3 + s/3 + s/3}}{{\dfrac{{s/3}}{{{v_1}}} + \dfrac{{s/3}}{{{v_2}}} + \dfrac{{s/3}}{{{v_3}}}}} \\= \dfrac{1}{{\dfrac{{1/3}}{{14}} + \dfrac{{1/3}}{{16}} + \dfrac{{1/3}}{8}}} = 11,6km/h\)
Một người đi xe máy từ A đến B. Trên đoạn đường đầu người đó đi hết 15 phút. Đoạn đường còn lại người đó đi trong thời gian 30 phút với vận tốc 12m/s. Hỏi đoạn đường đầu dài bao nhiêu? Biết vận tốc trung bình của người đó trên cả quãng đường AB là 36km/h. Hãy chọn câu trả lời đúng.
Thời gian đi từ A đến B: \(t = {t_1} + {t_2} = 45phut = \dfrac{3}{4}\,\left( h \right)\)
Độ dài AB : \(S = {v_{tb}}.t = 36.\dfrac{3}{4} = 27km\)
Độ dài của đoạn đường sau là : \({S_2} = {v_2}.{t_2} = 12.30.60 = 21600m = 21,6km\)
Độ dài đoạn đường đầu là : \({S_1} = S - {S_2} = 27 - 21,6 = 5,4km\)
Hai ô tô chuyển động thẳng đều khởi hành đồng thời ở 2 địa điểm cách nhau 20km. Nếu đi ngược chiều thi sau 15 phút chúng gặp nhau. Nếu đi cùng chiều sau 30 phút thì chúng đuổi kịp nhau. Vận tốc của hai xe đó là:
Cách giải:
Gọi v1 và v2 là vận tốc của hai ô tô
- Hai ô tô chuyển động ngược chiều đến gặp nhau tại C


Ta có: \(\left\{ \begin{array}{l}{s_1} = AC = {v_1}t = {v_1}.0,25\,\,\left( {km} \right)\\{s_2} = BC = {v_2}t = {v_2}.0,25\,\,\left( {km} \right)\end{array} \right.\)
Có: \(AB + BC = AB \Leftrightarrow 0,25{v_1} + 0,25{v_2} = 20\,\,\,\,\left( 1 \right)\)
- Hai ô tô chuyển động cùng chiều (v1 > v2)

Ta có: \(\left\{ \begin{array}{l}{s_1} = AC = {v_1}t = {v_1}.0,5\,\,\left( {km} \right)\\{s_2} = BC = {v_2}t = {v_2}.0,5\,\,\left( {km} \right)\end{array} \right.\)
Có: \(AC - BC = AB \Leftrightarrow 0,5{v_1} - 0,5{v_2} = 20\,\,\,\,\left( 2 \right)\)
- Từ (1) và (2) ta có: \(\left\{ \begin{array}{l}0,25{v_1} + 0,25{v_2} = 20\\0,5{v_1} - 0,5{v_2} = 20\,\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{v_1} = 60km/s\\{v_2} = 20km/h\end{array} \right.\)

