Ôn tập về số tự nhiên

1. Dãy số tự nhiên

a) Dãy số tự nhiên

- Các số: \(0\,\,;\,\,1\,\,;\,\,2\,\,;\,\,3\,\,;\,\,...\,\,;\,\,9\,\,;\,\,10\,\,;\,\,...\,\,;\,\,100\,\,;\,\,...\,\,;\,\,1000\,\,;\,\,...\) là các số tự nhiên.

- Các số tự nhiên sắp xếp theo thứ tự từ bé đến lớn tạo thành dãy số tự nhiên:

\(0\,\,;\,\,1\,\,;\,\,2\,\,;\,\,3\,\,;\,\,4\,\,;\,\,5\,\,;\,\,6\,\,;\,\,7\,\,;\,\,8\,\,;\,\,9\,\,;\,\,10\,\,;\,\,...\)

- Có thể biểu diễn dãy số tự nhiên trên tia số:

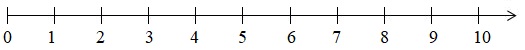
Số \(0\) ứng với điểm gốc của tia số. Mỗi số tự nhiên ứng với một điểm trên tia số.

- Trong dãy số tự nhiên:

+ Thêm \(1\) vào bất cứ số nào cũng được số tự nhiên liền sau số đó. Vì vậy, không có số tự nhiên lớn nhất và dãy số tự nhiên có thể kéo dài mãi.

Chẳng hạn, số \(1000\) thêm \(1\) được số tự nhiên liền sau là \(1001\), số \(1001\) thêm \(1\) được số tự nhiên liền sau là \(1002\), …

+ Bớt \(1\) vào bất kì số nào (khác số \(0\)) cũng được số tự nhiên liền trước số đó.

Chẳng hạn, bớt \(1\) ở số \(1\) được số tự nhiên liền trước  là số \(0\).

b) Viết số tự nhiên trong hệ thập phân

Trong cách viết số tự nhiên:

-  Ở mỗi hàng có thể viết được một chữ số. Cứ mười đơn vị ở một hàng lại hợp thành một đơn vị ở hàng trên tiếp liền nó.

Chẳng hạn:      \(10\) đơn vị \( = \,\,1\) chục

                       \(10\) chục \( = \,\,1\) trăm

                       \(10\) trăm \( = \,\,1\) nghìn

Chẳng hạn:      Số “chín trăm chín mươi chín” viết là: \(999\)

                       Số “hai nghìn không trăm linh năm” viết là: \(2005\)

Số “sáu trăm tám mươi lăm triệu bốn trăm linh hai nghìn bảy trăm chín mươi ba” viết là: \(685\,\,402\,\,793\).

Nhận xét: Giá trị của mỗi chữ số phụ thuộc vào vị trí của nó trong số đó.

Chẳng hạn, số \(111\) có ba chữ số \(1\), kể từ phải sang trái mỗi chữ số \(1\) lần lượt nhận giá trị là \(1\,;\,\,10\, ;\,\,100\).

Viết số tự nhiên với các đặc điểm trên được gọi là viết số tự nhiên trong hệ thập phân.

2. Hàng và lớp

Hàng đơn vị, hàng chục, hàng trăm hợp thành lớp đơn vị.

Hàng nghìn, hàng chục nghìn, hàng trăm nghìn hợp thành lớp nghìn.

Hàng triệu, chục triệu, trăm triệu hợp thành lớp triệu.

3. So sánh các số tự nhiên

 Trong hai số tự nhiên:

- Số nào có nhiều chữ số hơn thì số kia lớn hơn. Số nào có ít chữ số hơn thì bé hơn.

- Nếu hai số có chữ số bằng nhau thì so sánh từng cặp chữ số ở cùng một hàng kể từ trái sang phải.

- Nếu hai số có tất cả các cặp chữ số ở từng hàng đều bằng nhau thì hai số đó bằng nhau.

4. Một số dấu hiệu chia hết

a) Dấu hiệu chia hết cho \(2\)

Các số có chữ số tận cùng là \(0\,;\,\,2\,;\,\,4\,;\,\,6\,;\,\,8\) thì chia hết cho \(2\).

b) Dấu hiệu chia hết cho \(5\):

Các số có chữ số tận cùng là \(0\,;\,\,5\) thì chia hết cho \(5\).

c) Dấu hiệu chia hết cho \(9\):

Các số có tổng các chữ số chia hết cho \(9\) thì chia hết cho \(9\).

d) Dấu hiệu chia hết cho \(3\):

Các số có tổng các chữ số chia hết cho \(3\) thì chia hết cho \(3\).