1. Phân số và phép chia số tự nhiên
a) Có \(8\) quả cam, chia đều cho \(4\) Mỗi em được:
\(8:4 = 2\) (quả cam)
b) Có \(3\) cái bánh, chia đều cho \(4\) Hỏi mỗi em được bao nhiêu phần của cái bánh?
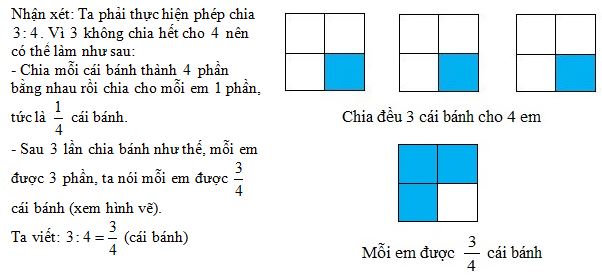
c) Nhận xét:
Thương của phép chia số tự nhiên cho số tư nhiên (khác \(0\)) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
Chẳng hạn: \(8:4 = \dfrac{8}{4}\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,3:4 = \dfrac{3}{4}\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,5:5 = \dfrac{5}{5}\,\, \cdot \)
2. Phân số lớn hơn \(1\), bằng \(1\), nhỏ hơn \(1\)
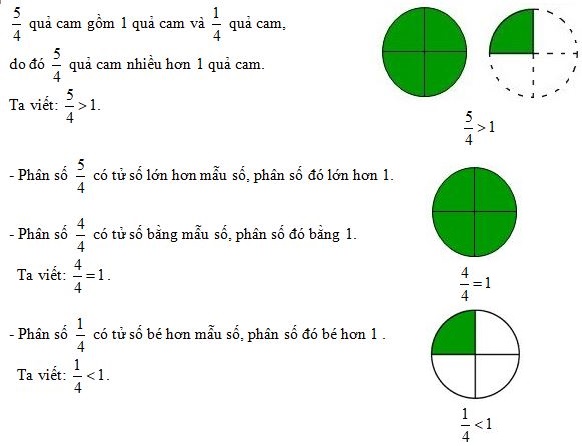
a) Ví dụ 1: Có \(2\) quả cam, chia mỗi quả cam thành \(4\) phần bằng nhau. Vân ăn \(1\) quả cam và \(\dfrac{1}{4}\) quả cam. Viết phân số chỉ số phần quả cam Vân đã ăn.
Ta thấy: Ăn \(1\) quả cam, tức là ăn \(4\) phần hay \(\dfrac{4}{4}\) quả cam; ăn thêm \(\dfrac{1}{4}\) quả cam nữa, tức là ăn thêm 1 phần, như vậy Vân đã ăn tất cả \(5\) phần hay \(\dfrac{5}{4}\) quả cam.
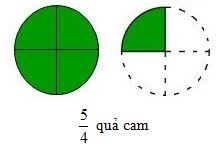
b) Ví dụ 2: Chia đều \(5\) quả cam cho \(4\) người. Tìm phần cam của mỗi người.
Ta có thể làm như sau: Chia mỗi quả cam thành \(4\) phần bằng nhau. Lần lượt đưa cho mỗi người \(1\) phần, tức là \(\dfrac{1}{4}\) của từng quả cam. Sau \(5\) lần chia như thế, mỗi người được \(5\) phần hay \(\dfrac{5}{4}\) quả cam.
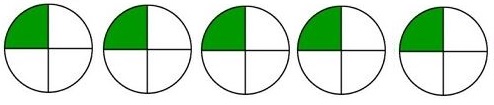
Vậy: \(5:4 = \dfrac{5}{4}\) (quả cam)
c) Nhận xét:
- Kết quả của phép chia số tự nhiên cho số tự nhiên (khác \(0\)) có thế viết là một phân số, chẳng hạn: \(5:4 = \dfrac{5}{4}\, \cdot \)