I. Lực - Tổng hợp và phân tích lực
I - LỰC - CÂN BẰNG LỰC
Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.
- Lực \(\overrightarrow F \) có:
+ Điểm đặt: nằm tại vật chịu tác dụng của lực
+ Phương, chiều: trùng với véctơ biểu diễn lực
+ Độ lớn lực: tỉ lệ với độ dài của véctơ biểu diễn lực

- Hai lực cân bằng là hai lực cùng tác dụng lên một vật, cùng giá, cùng độ lớn và ngược chiều.
- Đơn vị của lực là Niutơn (N).
* Điều kiện cân bằng của một chất điểm
Hợp của tất cả các lực tác dụng lên nó bằng \(\overrightarrow 0 \)
\(\overrightarrow F = {\overrightarrow F _1} + {\overrightarrow F _2} + ... + {\overrightarrow F _n} = \overrightarrow 0 \)
II - TỔNG HỢP LỰC
1. Định nghĩa
Tổng hợp lực là thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt các lực ấy.
Lực thay thế này gọi là hợp lực.
2. Qui tắc hình bình hành.
Nếu hai lực đồng qui làm thành hai cạnh của một hình bình hành, thì đường chéo kể từ điểm đồng qui biểu diễn hợp lực của chúng.
\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
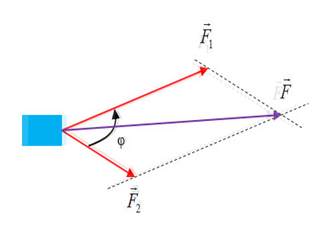
III - PHÂN TÍCH LỰC
Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
Các lực thay thế gọi là các lực thành phần.
IV - CÁC DẠNG BÀI TẬP
1. Tổng hợp lực
a. Tổng hợp lực của 2 lực thành phần: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
- Bước 1: Tịnh tiến các lực về cùng điểm đặt
- Bước 2: Nếu các lực không cùng phương thì sử dụng quy tắc hình bình hành để xác định véctơ tổng trên hình vẽ.
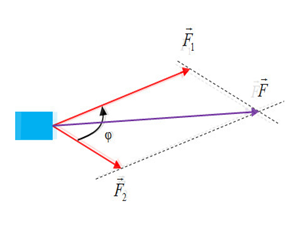
- Bước 3: Sử dụng biểu thức sau để xác định độ lớn lực tổng hợp
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\varphi } \)
* Các trường hợp đặc biệt:
- \({\overrightarrow F _1} \uparrow \uparrow {\overrightarrow F _2} \to F = {F_1} + {F_2}\)
- \({\overrightarrow F _1} \uparrow \downarrow {\overrightarrow F _2} \to F = \left| {{F_1} - {F_2}} \right|\)
- \({\overrightarrow F _1} \bot {\overrightarrow F _2} \to F = \sqrt {{F_1}^2 + {F_2}^2} \)
\(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)
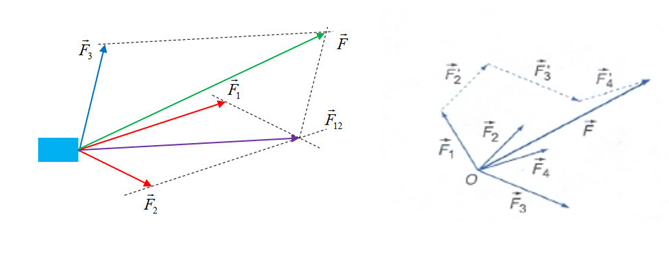
b. Tổng hợp lực của 3 lực thành phần
* Cách 1:
- Bước 1: Chọn hệ trục tọa độ Oxy
- Bước 2: Xác định các góc: \(\left( {{{\overrightarrow F }_1}{\rm{,Ox}}} \right) = {\alpha _1};\left( {{{\overrightarrow F }_2}{\rm{,Ox}}} \right) = {\alpha _2};...\)
- Bước 3: Tìm hình chiếu của các lực trên trục Ox, Oy:
\(\left\{ \begin{array}{l}{F_x} = {F_1}{\rm{cos}}{\alpha _1} + {F_2}{\rm{cos}}{\alpha _2} + ...\\{F_y} = {F_1}\sin {\alpha _1} + {F_2}\sin {\alpha _2} + ...\end{array} \right.\)
- Bước 3: Xác định độ lớn của hợp lực bởi công thức: \(F = \sqrt {F_x^2 + F_y^2} \) và \(\left( {\overrightarrow F {\rm{,Ox}}} \right) = \alpha \)
với \(\left[ \begin{array}{l}\tan \alpha = \frac{{{F_y}}}{{{F_x}}} \Leftrightarrow {F_x}{F_y} > 0\\\tan \alpha = - \frac{{{F_y}}}{{{F_x}}} \Leftrightarrow {F_x}{F_y} < 0\end{array} \right.\)
* Cách 2:
- Bước 1: Tổng hợp 2 lực 1
- Bước 2: Tổng hợp với lực thành phần còn lại
Sử dụng quy hình bình hành hoặc quy tắc đa giác
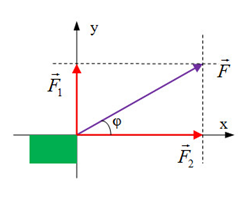
2. Phân tích lực
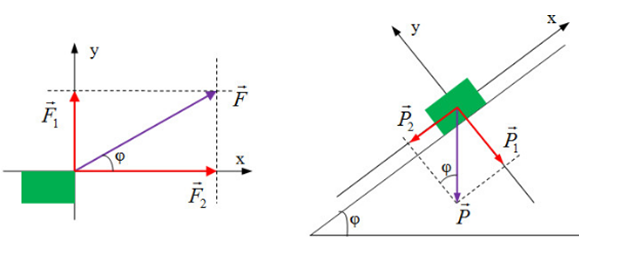
Căn cứ vào vị trí góc \(\varphi \) xác định được độ lớn của các lực thành phần:
\(\left\{ \begin{array}{l}{F_1} = F\sin \varphi \\{F_2} = Fc{\rm{os}}\varphi \end{array} \right.\) ; \(\left\{ \begin{array}{l}{P_1} = Pc{\rm{os}}\varphi \\{P_2} = P\sin \varphi \end{array} \right.\)
II. Ba định luật Newton
I - ĐỊNH LUẬT I NIU-TƠN
1. Định luật I - Niutơn
Nếu một vật không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không, thì nó giữ nguyên trạng thái đứng yên hoặc chuyển động thẳng đều
2. Quán tính
Là tính chất vật lý gắn liền với mọi vật chuyển động, nó có xu hướng bảo toàn vận tốc của vật cả về hướng và độ lớn.
- Biểu hiện của quán tính
+ Xu hướng giữ nguyên trạng thái đứng yên => Ta nói vật có “tính ì”
+ Xu hướng giữ nguyên trạng thái chuyển động => Ta nói vật chuyển động có “đà”
3. Hệ quy chiếu quán tính
Là hệ quy chiếu gắn vào vật mốc đứng yên hoặc chuyển động thẳng đều.
Trong hệ quy chiếu quán tính không có lực quán tính.
4. Hệ quy chiếu phi quán tính
Là hệ quy chiếu gắn vào vật mốc chuyển động có gia tốc.
Trong hệ quy chiếu phi quán tính xuất hiện lực quán tính
II- ĐỊNH LUẬT II NIU-TƠN
1. Định luật
Véctơ gia tốc của một vật luôn cùng hướng với lực tác dụng lên vật. Độ lớn của véctơ gia tốc tỉ lệ thuận với độ lớn của véctơ lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật.
\(\overrightarrow a = \frac{{\overrightarrow F }}{m}\) hay \(\overrightarrow F = m\overrightarrow a \)
Trong đó:
+ \(\overrightarrow F = {\overrightarrow F _1} + {\overrightarrow F _2} + ... + {\overrightarrow F _n}\) hợp của các lực tác dụng vào vật (N)
+ m: khối lượng của vật (kg)
+ a: gia tốc của vật (m/s2)
Các yếu tố của véctơ lực:
- Điểm đặt là vị trị mà lực đặt lên vật
- Phương, chiều: là phương và chiều của gia tốc mà lực gây ra cho vật
- Độ lớn: \(F = ma\)
- Đơn vị: N (Niutơn) \((1N = 1kg.m/{s^2})\)
2. Khối lượng và mức quán tính.
Khối lượng của vật là đại lượng đặc trưng cho mức quán tính của vật.
Vật có khối lượng càng lớn thì mức quán tính càng lớn và ngược lại
- Tính chất của khối lượng:
+ Khối lượng là một đại lượng vô hướng, dương và không đổi đối với mỗi vật.
+ Khối lượng có tính chất cộng.
3. Trọng lượng.
Trọng lượng (độ lớn của trọng lực) của vật tỉ lệ thuận với khối lượng của nó.
\(\overrightarrow P = m\overrightarrow g \)
- Trong lượng P luôn hướng thẳng đứng xuông dưới và có độ lớn: \(P = mg\)
- Điều kiện cân bằng của một chất điểm
Hợp của tất cả các lực tác dụng lên nó bằng \(\overrightarrow 0 \)
\(\overrightarrow F = {\overrightarrow F _1} + {\overrightarrow F _2} + ... + {\overrightarrow F _n} = \overrightarrow 0 \)
III- ĐỊNH LUẬT III - NEWTON
1. Sự tương tác giữa các vật
Khi một vật tác dụng lên vật khác một lực thì vật đó cũng bị vật kia tác dụng ngược trở lại một lực. Ta nói giữa 2 vật có sự tương tác.
2. Định luật
Khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng trở lại vật A một lực. Hai lực này là hai lực trực đối.
\({\overrightarrow F _{AB}} = - {\overrightarrow F _{BA}}\)

3. Lực và phản lực
Một trong hai lực tương tác giữa hai vật gọi là lực tác dụng còn lực kia gọi là phản lực.
Đặc điểm của lực và phản lực :
+ Lực và phản lực luôn luôn xuất hiện (hoặc mất đi) đồng thời.
+ Lực và phản lực có cùng giá, cùng độ lớn nhưng ngược chiều.
Hai lực có đặc điểm như vậy gọi là hai lực trực đối.
+ Lực và phản lực không cân bằng nhau vì chúng đặt vào hai vật khác nhau.

