I. Tổng hợp lực
Tổng hợp lực là phép thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy.
Lực thay thế này gọi là lực tổng hợp. Các lực được thay thế được gọi là các lực thành phần.
1. Tổng hợp hai lực cùng phương
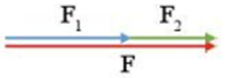
- Hai lực cùng phương, cùng chiều thì làm tăng tác dụng lên vật, độ lớn của hợp lực bằng:
\(F = {F_1} + {F_2}\)
- Hai lực cùng phương, ngược chiều thì chúng hạn chế, thậm chí triệt tiêu tác dụng của nhau lên vật và hợp lực có giá trị bằng:
\(F = {F_1} - {F_2}\)
Nếu F > 0 thì hợp lực F cùng chiều với lực thành phần F1
Nếu F < 0 thì hợp lực F ngược chiều với lực thành phần F1
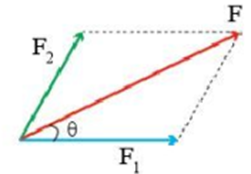
2. Tổng hợp các lực đồng quy – Quy tắc hình bình hành
- Để tổng hợp hai lực đồng quy \(\overrightarrow {{F_1}} \)và \(\overrightarrow {{F_2}} \) cùng đặt tại điểm O của vật, ta sử dụng quy tắc hình bình hành như sau:
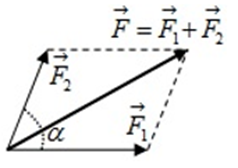
Bước 1: Vẽ hai vectơ \(\overrightarrow {{F_1}} \)và \(\overrightarrow {{F_2}} \)đồng quy tại 0
Bước 2: Từ 2 vectơ \(\overrightarrow {{F_1}} \)và \(\overrightarrow {{F_2}} \)vẽ hình bình hành có hai cạnh liền kề trùng với \(\overrightarrow {{F_1}} \)và \(\overrightarrow {{F_2}} \)
Bước 3: Vẽ đường chéo của hình bình hành có cùng gốc O. Vectơ hợp lực \(\overrightarrow F \)chính là đường chéo này.
- Độ lớn của vectơ hợp lực \(\overrightarrow F \)được xác định như sau: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
- Độ lớn của hợp lực:
\({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}co{\rm{s}}\alpha \)
- Hướng của hợp lực so với lực \({F_1}\)là: \(co{\rm{s}}\theta {\rm{ = }}\dfrac{{{F^2} + F_1^2 - F_2^2}}{{2{F_1}{F_2}}}\)
3. Tổng hợp hai lực vuông góc
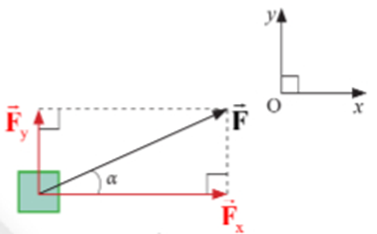
- Ta có vectơ hợp lực F: \(\overrightarrow F = \overrightarrow {{F_x}} + \overrightarrow {{F_y}} \)
- Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2} \)
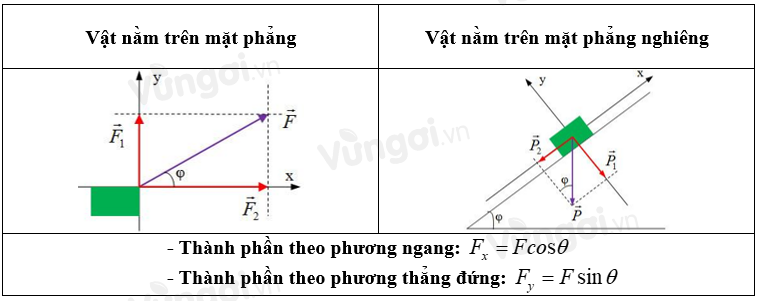
II. Phân tích lực
Phân tích lực là thay thế một lực bằng các lực thành phần có tác dụng giống hệt các lực đó.
Ta thường phân tích một lực thành hai lực thành phần vuông góc với nhau, có tác dụng độc lập với nhau.
