I. Đồ thị độ dịch chuyển - thời gian trong chuyển động thẳng
1. Cách vẽ đồ thị độ dịch chuyển – thời gian (d – t) trong chuyển động thẳng đều
- Biểu thức d = v.t, vẽ giống biểu thức hàm số y = a.x
- Hình dạng: đường thẳng
Ví dụ:
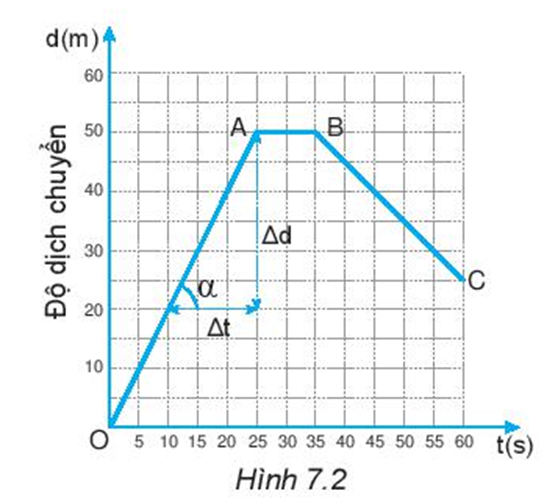
2. Sử dụng đồ thị độ dịch chuyển – thời gian trong chuyển động thẳng
Dựa vào đồ thị, ta có thể thu thập số liệu để tính toán yêu cầu của đề bài
3. Vận tốc và đồ thị độ dịch chuyển – thời gian trong chuyển động thẳng
- Độ dốc của độ dịch chuyển – thời gian trong chuyển động thẳng cho biết độ lớn vận tốc chuyển động
VD: Trong hình 7.2, vận tốc của vật trên đường thẳng OA là:
\(v = \dfrac{{\Delta d}}{{\Delta t}} = \dfrac{{50 - 20}}{{25 - 10}} = 2(m/s)\)
II. Độ dịch chuyển tổng hợp
- Độ dịch chuyển tổng hợp bằng tổng các độ dịch chuyển mà vật trải qua trong cả quá trình chuyển động
Ví dụ: Một ô tô đi 17 km theo hướng đông và sau đó đi 10 km về hướng bắc. Quãng đường ô tô đi được là 27 km. Tìm độ dịch chuyển tổng hợp của ô tô.
Cách giải:
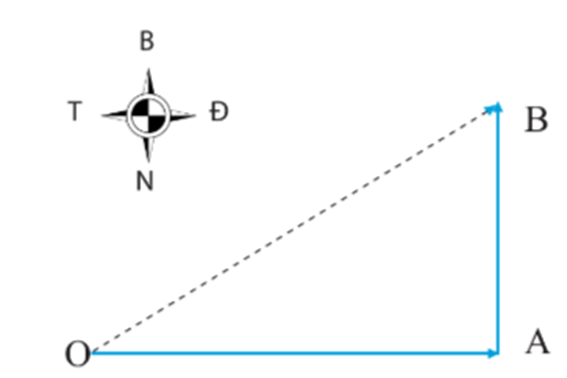
* Tìm độ lớn
Độ dịch chuyển tổng hợp được biểu diễn bằng vecto OB.
Vì góc giữa vecto OA và vecto AB là góc vuông, nên độ lớn của độ dịch chuyển tổng hợp được tính bằng:
\(\begin{array}{l}O{B^2} = O{A^2} + A{B^2} = {17^2} + {10^2} = 389\\ \Rightarrow OB = \sqrt {389} \approx 20(km)\end{array}\)
* Tìm hướng
Vì cạnh huyền của tam giác vuông có chiều dài gấp đôi cạnh góc vuông nên góc giữa vecto OB và vecto AB là 600
=> Độ dịch chuyển cuối cùng của ô tô là 20 km lệch so với hướng bắc góc 600 về phía đông
III. Vận tốc tổng hợp
- Nếu một vật tham gia đồng thời hai chuyển động theo hai phương và mỗi phương có một vận tốc thì vận tốc tổng hợp bằng tổng các vận tốc này
Ví dụ: Một vận động viên bơi về phía bắc với vận tốc 1,7 m/s, nước sông chảy với vận tốc 1,0 m/s về phía đông. Tìm độ lớn và hướng vận tốc tổng hợp của vận động viên
Cách giải:
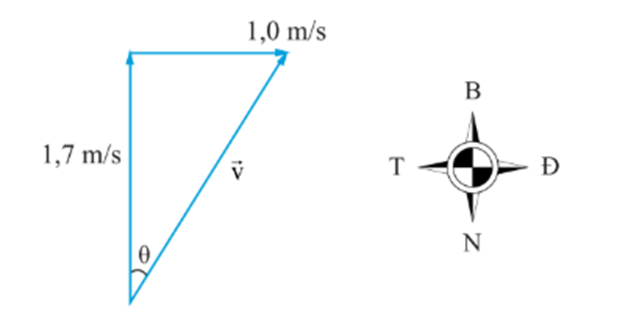
Ta có: \(v = \sqrt {1,{7^2} + {1^2}} = 1,97 \approx 2(m/s)\)
Do cạnh huyền gấp đôi cạnh góc vuông nên góc θ là 300
=> Vận tốc tổng hợp của vận động viên là 2 m/s và có hướng lệch so với hướng bắc 300 về phía đông.

