I. Gia tốc
- Đại lượng đặc trưng cho độ biến thiên của vận tốc theo thời gian được gọi là gia tốc
- Trong chuyển động thẳng, gia tốc trung bình được xác định theo biểu thức:
\({a_{tb}} = \dfrac{{\Delta v}}{{\Delta t}} = \dfrac{{{v_2} - {v_1}}}{{\Delta t}}\)
- Gia tốc tức thời tại một thời điểm có giá trị bằng độ dốc của tiếp tuyến của đồ thị vận tốc – thời gian (v – t) tại thời điểm đó.
- Đơn vị: m/s2
- Khi Δt rất nhỏ, gia tốc trung bình trở thành gia tốc tức thời có gốc tại vị trí của vật, hướng cùng hướng với độ biến thiên vận tốc \(\overrightarrow {\Delta v} \), độ dài tỉ lệ với độ lớn của vecto \(\overrightarrow {\Delta v} \) theo một tỉ xích xác định.
- Phân loại:
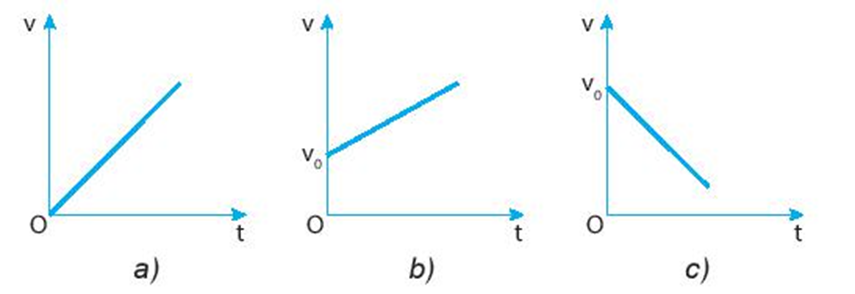
+ $a = 0$: chuyển động thẳng đều, vật có độ lớn vận tốc không đổi
+ $a \ne 0$ và bằng hằng số: chuyển động thẳng biến đổi đều, vật có độ lớn vận tốc thay đổi (tăng hoặc giảm) đều theo thời gian.
+ $a \ne 0$ nhưng không phải là hằng số: chuyển động thẳng biến đổi phức tạp (không xét trong chương trình THPT).
II. Đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều
Các dạng đồ thị vận tốc – thời gian trong chuyển động thẳng biến đổi đều
III. Độ dịch chuyển của chuyển động thẳng biến đổi đều
1. Tính độ dịch chuyển bằng đồ thị vận tốc – thời gian (v – t)
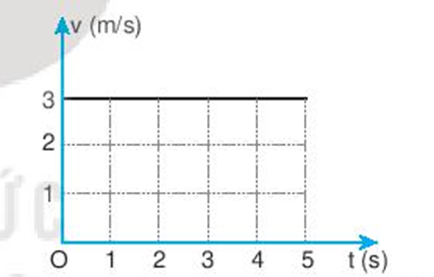
Nếu là đồ thị (v – t) của chuyển động thẳng đều thì độ dịch chuyển được tính bằng diện tích của hình chữ nhật được giới hạn của đồ thị (v – t) đối với trục hoành.
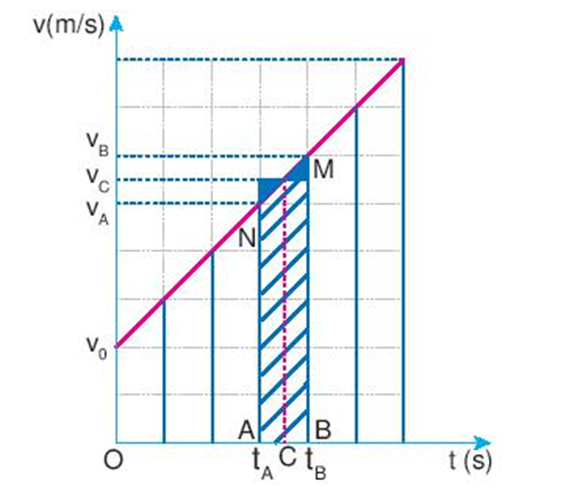
Nếu trong khoảng thời gian t, vật chuyển động thẳng biến đổi đều với vận tốc ban đầu là v0 thì công thức tính vận tốc là vt = v0 + a.t
=> Cách tính độ dịch chuyển
+ Kẻ đường thẳng song song với trục tung Ov, cách nhau một khoảng Δt rất nhỏ để chia hình thang giới hạn bởi đường thẳng biểu diễn đồ thị, đường thẳng vuông góc với trục Ot và các trục tọa độ thành các hình thang nhỏ có đường cao Δt
+ Chọn một hình thang nhỏ bất kì trong hình. Vì vật chuyển động thẳng biến đổi đều nên trong khoảng thời gian nhỏ từ tA đến tB , có thể coi là chuyển động thẳng với vận tốc \({v_C} = \dfrac{{{v_A} + {v_B}}}{2}\) (C nằm giữa A và B)
+ Độ dịch chuyển của vật trong thời gian Δt có độ lớn bằng diện tích hình chữ nhật có cạnh vC và Δt.
2. Tính độ dịch chuyển bằng công thức
+ Công thức tính độ dịch chuyển: \(d = {v_0}.t + \dfrac{1}{2}.a.{t^2}\)
+ Mối liên hệ giữa vận tốc, gia tốc và độ dịch chuyển: \(v_t^2 - v_0^2 = 2.a.d\)

