I. Các khái niệm cơ bản của chuyển động cơ học
I- CHUYỂN ĐỘNG CƠ
Chuyển động cơ là sự dời chỗ của vật theo thời gian
Khi vật dời chỗ thì có sự thay đổi khoảng cách giữa các vật và những vật khác được coi như đứng yên.
Vật đứng yên gọi là vật mốc.
- Chuyển động cơ có tính tương đối
II- CHẤT ĐIỂM
Chất điểm là vật có kích thước rất nhỏ so với khoảng cách mà ta xét
So với chiều dài của cái bàn thì con kiến được coi là một chất điểm
So với quãng đường từ Hà Nội đến Đà Nẵng các phương tiện chuyển động như xe đạp, xe máy, otô,.. được coi là chất điểm
...
- Quỹ đạo
Tập hợp tất cả các vị trí của một chất điểm chuyển động tạo ra một đường nhất đinh. Đường này gọi là quỹ đạo của chuyển động.
- Hệ tọa độ:
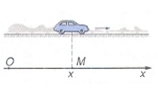
- Vị trí của một chất điểm
Để xác định vị trí của một chất điểm, người ta chọn một vật mốc, gắn vào đó một hệ tọa độ, vị trí của chất điểm được xác định bằng tọa độ của nó trong hệ tọa độ này.
III- THỜI GIAN
- Mốc thời gian (gốc thời gian): là thời điểm mà ta bắt đầu đo thời gian
- Thời điểm: giá trị mà đồng hồ hiện đang chỉ đến theo một mốc cho trước mà ta xét.
- Thời gian: là khoảng thời gian trôi đi trong thực tế giữa hai thời điểm mà ta xét
- Dụng cụ đo thời gian: Đồng hồ
IV- HỆ QUY CHIẾU
Một vật mốc gắn với một hệ tọa độ và một gốc thời gian cùng với một đồng hồ hợp thành một hệ quy chiếu
Hệ quy chiếu = Hệ tọa độ gắn với vật mốc + đồng hồ và gốc thời gian
V- CHUYỂN ĐỘNG TỊNH TIẾN
Chuyển động tịnh tiến, mọi điểm của nó có quỹ đạo giống hệt nhau, có thể chồng khít lên nhau được.
II. Phân biệt độ dịch chuyển và quãng đường đi được
- Độ dịch chuyển là khoảng cách từ vị trí đầu đến vị cuối của vật, cho biết độ dài và sự thay đổi vị trí của vật
- Quãng đường là độ dài của vật thực hiện được trong suốt quá trình chuyển động.
Ví dụ: Một vật di chuyển từ A đến B được 500 m, rồi quay về C là 150 m. Hỏi độ dịch chuyển và quãng đường của vật này là bao nhiêu?
Cách giải:
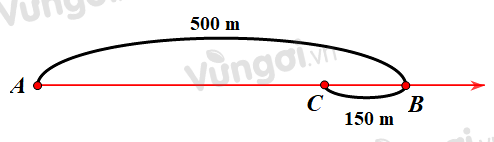
Độ dịch chuyển: \(\overline d = AC = 500 - 150 = 350(m)\)
Quãng đường: s = AB + BC = 500 + 150 = 650 (m).
Độ dịch chuyển và quãng đường bằng nhau khi vật chuyển động không đổi chiều và chuyển động thẳng.
III. Tốc độ
1. Tốc độ trung bình
- Khái niệm: là quãng đường đi được trong cùng một đơn vị thời gian để xác định độ nhanh, chậm của chuyển động
- Biểu thức: \(v = \dfrac{s}{t}\)
- Đơn vị: m/s; km/h
=> Quãng đường đo được: s = v.t
=> Thời gian đi: \(t = \dfrac{s}{v}\)
Chú ý:
+ Nếu s đơn vị là m, t đơn vị là s thì v có đơn vị là m/s
+ Nếu s đơn vị là km, t đơn vị là h thì v có đơn vị là km/h
+ 1 m/s = 3,6 km/h.
2. Tốc độ tức thời
- Khái niệm: Tốc độ tức thời là tốc độ trung bình đo được trong một khoảng thời rất ngắn (tốc độ tại một thời điểm xác định).
- Tốc độ tức thời diễn tả sự nhanh, chậm của chuyển động tại thời điểm đó.
Ví dụ: Trên xe máy và ô tô, đồng hồ tốc độ (tốc kế) đặt trước mặt người lái xe, chỉ tốc độ mà xe đang chạy vào thời điểm, tốc độ đó là tốc độ tức thời.
3. Đơn vị đo tốc độ
|
s |
m |
km |
dặm |
|
t |
s |
h |
phút |
|
vtb |
m/s |
km/h |
dặm/phút |
IV. Vận tốc
1. Vận tốc trung bình
- Khái niệm: vận tốc trung bình được xác định bằng thương số của độ dịch chuyển và thời gian dịch chuyển để xác định độ nhanh, chậm của chuyển động theo một hướng xác định.
- Kí hiệu: \(\overrightarrow v \)
- Biểu thức: \(\overrightarrow v = \dfrac{{\overrightarrow d }}{t} = \dfrac{{\overrightarrow {\Delta x} }}{t}\)
- Đơn vị: m/s; km/h
- Vì độ dịch chuyển là một đại lượng vectơ nên vận tốc cũng là một đại lượng vectơ. Vectơ vận tốc có:
+ Gốc nằm trên vật chuyển động
+ Hướng là hướng của độ dịch chuyển
+ Độ dài tỉ lệ với độ lớn của vận tốc.
- Phân biệt giữa vận tốc và tốc độ
- Tốc độ trung bình chỉ bằng độ lớn của vận tốc trung bình khi vật chuyển động thẳng không đổi chiều.
- Xét trong thời gian rất nhỏ, vận tốc trung bình trở thành vận tốc tức thời. Độ lớn của vận tốc tức thời chính là tốc độ tức thời
2. Vận tốc tức thời
- Khái niệm: Vận tốc tức thời là vận tốc tại một thời điểm xác định, được kí hiệu là \(\overrightarrow {{v_t}} \)
- Biểu thức: \(\overrightarrow {{v_t}} = \dfrac{{\Delta \overrightarrow d }}{{\Delta t}}\) với Δt rất nhỏ.
3. Tổng hợp vận tốc
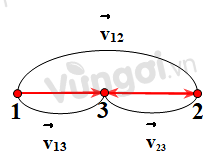
(1) là vật chuyển động đang xét.
(2) là vật chuyển động được chọn làm gốc của hệ quy chiếu chuyển động
(3) là vật đứng yên được chọn gốc của hệ quy chiếu đứng yên.
Ta có \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
* Trường hợp 1: Nếu \(\overrightarrow {{v_{12}}} \) cùng chiều với \(\overrightarrow {{v_{23}}} \) thì:
\({v_{13}} = {v_{12}} + {v_{23}}\)
* Trường hợp 2: Nếu \(\overrightarrow {{v_{12}}} \) ngược chiều với \(\overrightarrow {{v_{23}}} \) thì:
\({v_{13}} = \left| {{v_{12}} - {v_{23}}} \right|\)
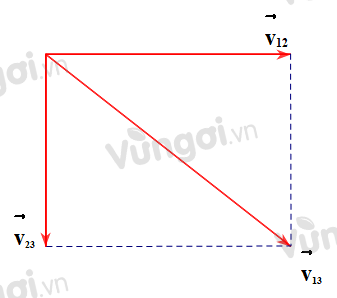
* Trường hợp 3: Nếu \(\overrightarrow {{v_{12}}} \) vuông góc với \(\overrightarrow {{v_{23}}} \) thì:
\(v_{13}^2 = v_{12}^2 + v_{23}^2\)
V. Tính tương đối của chuyển động - Công thức cộng vận tốc
I - TÍNH TƯƠNG ĐỐI CỦA CHUYỂN ĐỘNG
1. Tính tương đối của quỹ đạo
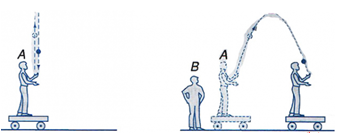
Quỹ đạo của chuyển động có tính tương đối, quỹ đạo trong các hệ quy chiếu khác nhau là khác nhau.
2. Tính tương đối của vận tốc.
Vận tốc của chuyển động có tính tương đối, vận tốc trong các hệ quy chiếu khác nhau là khác nhau.
II - CÔNG THỨC CỘNG VẬN TỐC
1. Hệ qui chiếu đứng yên và hệ qui chiếu chuyển động
- Hệ qui chiếu gắn với vật đứng yên gọi là hệ qui chiếu đứng yên.
- Hệ qui chiếu gắn với vật vật chuyển động gọi là hệ qui chiếu chuyển động.
2. Công thức cộng vận tốc.
\(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Trong đó:
+ Số 1: gắn với vật cần tính vận tốc
+ Số 2: gắn với hệ quy chiếu là các vật chuyển động
+ Số 3: gắn với hệ quy chiếu là các vật đứng yên
+ \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối
+ \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên gọi là vận tốc tuyệt đối.
- Độ lớn của vận tốc tuyệt đối:
\({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2 + 2{v_{12}}{v_{23}}{\rm{cos}}\alpha } \) với \(\alpha = \left( {\overrightarrow {{v_{12}}} ,\overrightarrow {{v_{23}}} } \right)\)
- Các trường hợp đặc biệt:
- \(\overrightarrow {{v_{12}}} \uparrow \uparrow \overrightarrow {{v_{23}}} \to {v_{13}} = v{}_{12} + {v_{23}}\)
- \(\overrightarrow {{v_{12}}} \uparrow \downarrow \overrightarrow {{v_{23}}} \to {v_{13}} = \left| {v{}_{12} - {v_{23}}} \right|\)
- \(\overrightarrow {{v_{12}}} \bot \overrightarrow {{v_{23}}} \to {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} \)
