I. Chuyển động thẳng biến đổi đều
I - CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
1. Định nghĩa
Chuyển động thẳng biến đổi là chuyển động thẳng trong đó gia tốc tức thời không đổi
2. Các phương trình của chuyển động thẳng biến đổi đều
- Gia tốc:
\(\overrightarrow a = \dfrac{{\overrightarrow v - \overrightarrow {{v_0}} }}{{\Delta t}}\) có độ lớn: \(a = \dfrac{{v - {v_0}}}{{\Delta t}}\)
- Phương trình tọa độ - thời gian của chuyển động thẳng biến đổi đều
\(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)
Trong đó:
+ x0 : tọa độ ban đầu của chất điểm
+ v0: Vận tốc của chất điểm tại thời điểm ban đầu (tại t = 0)
+ t: thời gian chuyển động
- Phương trình vận tốc:
\(v = {v_0} + at\)
Trong đó:
+ v0: Vận tốc của chất điểm tại thời điểm ban đầu (tại t = 0)
+ a: gia tốc
+ t: thời gian chuyển động
- Hệ thức độc lập thời gian:
\({v^2} - v_0^2 = 2{\rm{a}}\Delta {\rm{x}}\)
\((\Delta x = x - {x_0})\) là độ dời trong khoảng thời gian từ 0 đến t
II- ĐỒ THỊ CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
1. Đồ thị tọa độ theo thời gian (x - t)
Là nhánh parabol
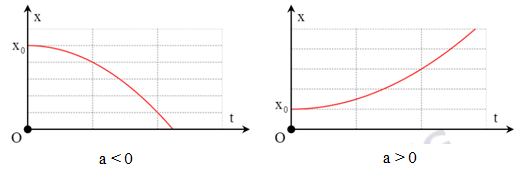
2. Đồ thị vận tốc theo thời gian (v - t)
Là đường thẳng xiên góc.
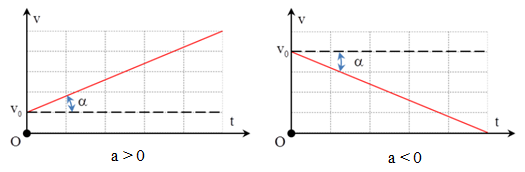
Hệ số góc của đường biểu diễn v - t bằng gia tốc của chuyển động: \(a = \tan \alpha = \frac{{v - {v_0}}}{t}\)
3. Đồ thị gia tốc theo thời gian (a - t)
Là đường thẳng song song với trục Ot
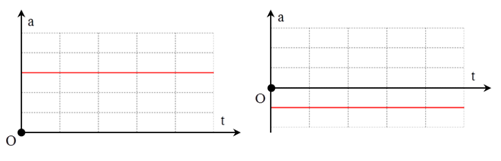
II. Các phương trình của chuyển động thẳng biến đổi đều
- Phương trình vận tốc: \(v = {v_0} + at\)
- Phương trình độ dịch chuyển: \(d = {v_0}.t + \dfrac{1}{2}.a.{t^2}\)
- Phương trình tọa độ: \(x = {x_0} + {v_0}.t + \dfrac{1}{2}.a.{t^2}\)
- Phương trình liên hệ giữa gia tốc, vận tốc và độ dịch chuyển: \({v^2} - v_0^2 = 2.a.d\)
III. Công thức của chuyển động thẳng biến đổi đều
Chuyển động thẳng với gia tốc không đổi được gọi là chuyển động thẳng biến đổi đều
1. Công thức tính vận tốc
Đồ thị vận tốc – thời gian biểu diễn chuyển động của một vật với vận tốc tăng dần đều từ v0 đến v trong thời gian t
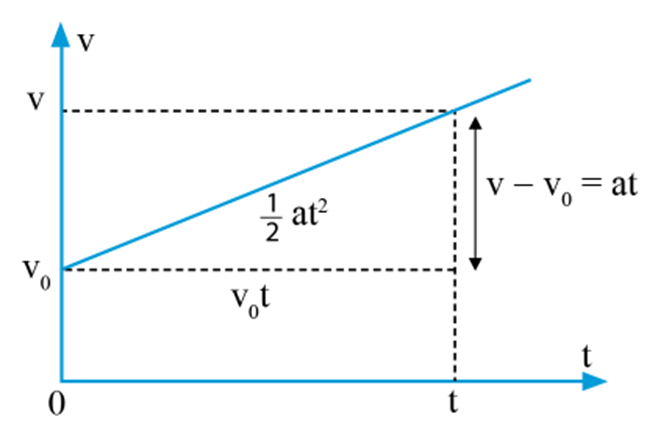
Độ dốc của đường thẳng có giá trị bằng gia tốc
\(a = \dfrac{{v - {v_0}}}{t} \Rightarrow v = {v_0} + a.t\) (1)
2. Công thức tính độ dịch chuyển
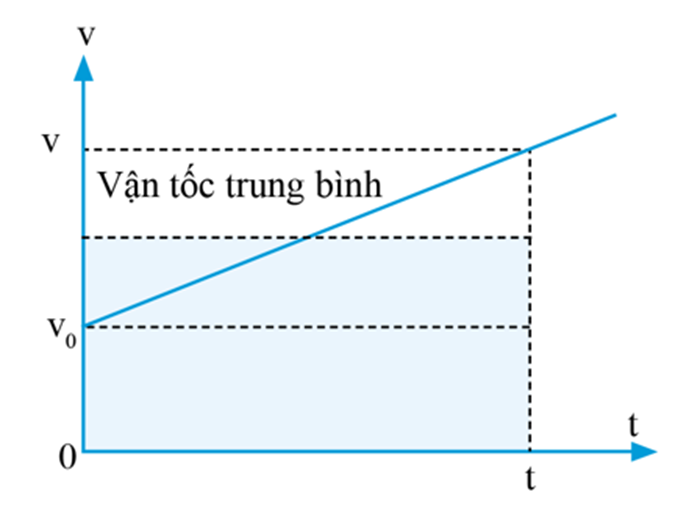
Vận tốc trung bình = \(\dfrac{{{v_0} + v}}{2}\)
Độ dịch chuyển = vận tốc trung bình x thời gian
=> Độ dịch chuyển: \(d = \dfrac{{{v_0} + v}}{2}.t\) (2)
3. Công thức tính quãng đường
Trong chuyển động theo một chiều xác định, độ dịch chuyển chính là quãng đường
Thay (1) và (2), ta có:
\(s = \dfrac{{{v_0} + {v_0} + at}}{2}.t \Rightarrow s = {v_0}.t + \dfrac{1}{2}.a.{t^2}\)
4. Công thức liên hệ quãng đường, vận tốc và gia tốc
Từ (1) và (2), ta có:
\(s = \dfrac{{{v_0} + v}}{2}.\dfrac{{v - {v_0}}}{a}\) hay \(s = \dfrac{{{v^2} - v_0^2}}{{2a}}\)
\( \Rightarrow {v^2} - v_0^2 = 2as\)
