Bài tập động lượng và định luật bảo toàn động lượng

I. Lý thuyết động lượng - định luật bảo toàn động lượng

1. Động lượng

- Động lượng là đại lượng đặc trưng cho khả năng truyền chuyển động của vật này lên vật khác thông qua tương tác giữa chúng.

- Động lượng của một vật có khối lượng m đang chuyển động với vận tốc v là đại lượng được đo bằng tích của khối lượng:

$\overrightarrow p  = m\overrightarrow v$

- Đặc điểm:

+ Là đại lượng vectơ

+ Cùng hướng với vectơ của vật

- Xung của lực $\overrightarrow F$ tác dụng lên vật trong khoảng $\Delta t$: $\overrightarrow F .\Delta t\left( {N.s} \right)$

- Xung lượng của lực tác dụng lên vật trong khoảng thời gian bằng độ biến thiên động lượng của vật trong khoảng thời gian đó: $\overrightarrow F \Delta t = \Delta \overrightarrow p$ hay $\overrightarrow F  = \dfrac{{\Delta \overrightarrow p }}{{\Delta t}}$

2. Định luật bảo toàn động lượng

* Các loại va chạm thường gặp

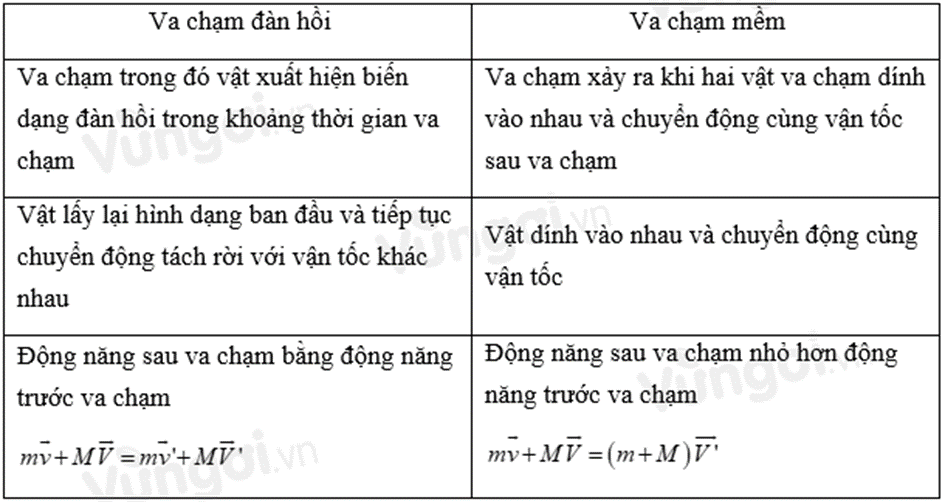
* Chuyển động bằng phản lực:

$m\overrightarrow v  + M\overrightarrow V  = \overrightarrow 0  \Rightarrow \overrightarrow V  =  - \dfrac{m}{M}\overrightarrow v$

II. Các dạng bài tập động lượng - định luật bảo toàn động lượng

Dạng 1. Xác định tổng động lượng, độ biến thiên động lượng và lực tác dụng

* Phương pháp:

- Độ lớn của động lượng: $p = mv$

- Khi có hai động lượng: $\overrightarrow {{p_1}} ,\overrightarrow {{p_2}}$ ta có: $\overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}}$

Dạng 2. Bài toán vận dụng định luật bảo toàn động lượng

* Lưu ý khi giải:

a. Khi các vector động lượng thành phần (các vector vận tốc) cùng phương thì ta có biểu thức của định luật được biết như sau: ${m_1}{v_1} + {m_2}{v_2} = {m_1}{v_1}' + {m_2}{v_2}'$

- Quy ước chiều dương của chuyển động:

+ Nếu vật chuyển động theo chiều dương đã chọn: $v > 0$

+ Nếu vật chuyển động ngược chiều dương đã chọn: $v < 0$

b. Khi các vector động lượng thành phần (các vector vận tốc) không cùng phương thì ta cần sử dụng hệ thức vector $\overrightarrow {{p_s}} = \overrightarrow {{p_t}}$và biểu diễn trên hình vẽ.

c. Điều kiện để áp dụng định luật bảo toàn động lượng:

- Hệ là hệ kín (tổng ngoại lực tác dụng lên hệ bằng 0 hoặc ngoại lực tác dụng rất nhỏ so với nội lực)

- Thời gian tương tác ngắn

1. Bài toán đạn nổ

- Bước 1: Khi một viên đạn nổ thì nội năng là rất lớn nên được coi là hệ kín

- Bước 2: Áp dụng định luật bảo toàn động lượng: $\overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_s}}$(1)

- Bước 3: Vẽ hình biểu diễn

- Bước 4: Chuyển (1) sang dạng đại số và tính toán.

2. Bài toán va chạm của hệ vật

* Phương pháp:

- Bước 1: Xác định kiểu va chạm

- Bước 2: Biểu diễn hình và xác định động lượng trước và sau va chạm

- Bước 3: Áp dụng định luật bảo toàn trước và sau va chạm

- Bước 4: Chuyển biểu thức sang dạng đại số và tính toán