Tính góc giữa hai mặt phẳng $\left( {MCD} \right)$ và $\left( {ABCD} \right)$.

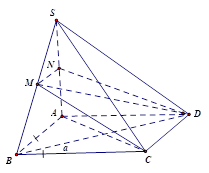
Bước 1:

Kẻ $MN\parallel AB\left( {N \in SA} \right)$

Mà $AB\parallel CD$

$\Rightarrow MN\parallel CD$ $\Rightarrow N \in \left( {MCD} \right)$

Bước 2:

$\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD \subset \left( {SAD} \right)\\CD \bot ND \subset \left( {SAD} \right)\end{array} \right.\\ \Rightarrow CD \bot \left( {SAD} \right)\end{array}$

Mặt khác,

$CD = \left( {MCD} \right) \cap \left( {ABCD} \right)$

$\Rightarrow \left( {SAD} \right)$ vuông góc với $\left( {MCD} \right)$ và $\left( {ABCD} \right)$.

Bước 3:

$\begin{array}{l}N \in \left( {MCD} \right) \Rightarrow ND \subset \left( {MCD} \right)\\N \in SA \subset \left( {SAD} \right) \Rightarrow ND \subset \left( {SAD} \right)\\ \Rightarrow ND = \left( {MCD} \right) \cap \left( {SAD} \right)\end{array}$

 $AD = \left( {ABCD} \right) \cap \left( {SAD} \right)$

$\Rightarrow \widehat {\left( {\left( {MCD} \right),\left( {ABCD} \right)} \right)}$$= \widehat {\left( {AD,ND} \right)} = \widehat {NDA} = \alpha$

Bước 4:

Xét tam giác NDA vuông tại N có: $AN = \dfrac{{SA}}{2} = a$, $AD = a$.

(do  $SA = \sqrt {S{D^2} - A{D^2}}  = \sqrt {5{a^2} - {a^2}}  = 2a$; N là trung điểm SA).

Nên $\Delta NAD$ vuông cân tại A $\Rightarrow \alpha  = 45^\circ$.

Vậy góc giữa $\left( {MCD} \right)$ và $\left( {ABCD} \right)$ bằng $45^\circ$