Câu hỏi:
2 năm trước
Một đội sản xuất phải làm 1000 sản phẩm trong một thời gian quy định. Nhờ tăng năng suất nên mỗi ngày đội làm thêm được 10 sản phẩm so với kế hoạch. Vì vậy, chẳng những đã làm vượt mức kế hoạch 80 sản phẩm mà còn hoàn thành sớm hơn 2 ngày so với quy định. Tính số sản phẩm mà đội phải làm trong 1 ngày theo kế hoạch.
Trả lời bởi giáo viên
Đáp án đúng: c
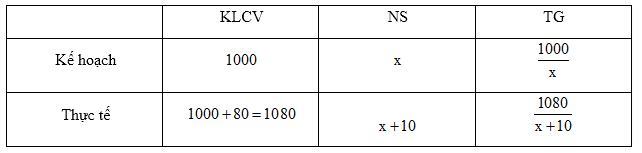
Gọi số sản phẩm đội dự định làm mỗi ngày là \(x\left( {x \in {N^*},\;x < 100} \right)\) (sản phẩm).
*) Theo kế hoạch
Thời gian hoàn thành là \(\dfrac{{1000}}{x}\) (ngày).
*) Thực tế.
Mỗi ngày tổ làm được\(x + 10\) ( sản phẩm).
Thời gian hoàn thành \(\dfrac{{1080}}{{x + 10}}\) ( ngày).
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{1000}}{x} - \dfrac{{1080}}{{x + 10}} = 2\\ \Leftrightarrow \dfrac{{500}}{x} - \dfrac{{540}}{{x + 10}} = 1\\ \Leftrightarrow \dfrac{{500(x + 10) - 540x}}{{x(x + 10)}} = \dfrac{{x(x + 10)}}{{x(x + 10)}}\\ \Rightarrow 500x + 5000 - 540x = {x^2} + 10x\\ \Leftrightarrow {x^2} + 50x - 5000 = 0\\\Delta ' = {25^2} - 1( - 5000) = 5625 > 0 \Rightarrow \sqrt {\Delta '} = 75\end{array}\)
Phương trình có hai nghiệm phân biệt : \({x_1} = - 25 - 75 = - 100\) (loại) và \({x_2} = - 25 + 75 = 50\)(tmđk).
Vậy theo kế hoạch, mỗi ngày tổ dự định làm \(50\) sản phẩm.
Hướng dẫn giải:
Các bước giải bài toán bằng cách lập phương trình:
+) Chọn ẩn và đặt điều kiện cho ẩn
+) Biểu thị các đại lượng chưa biết qua ẩn và các đại lượng đã biết.
+) Lập phương trình-giải phương trình.
+) Chọn kết quả và trả lời.
Pt: \(\dfrac{{1000}}{x} - \dfrac{{1080}}{{x + 10}} = 2\)
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
