Một ca nô xuôi dòng trên một khúc sông từ A đến B dài 80 km, sau đó lại ngược dòng đến địa điểm C cách B là 72 km, thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút. Tính vận tốc thực của ca nô biết vận tốc dòng nước là 4km/h.
Trả lời bởi giáo viên
Gọi vận tốc thực của ca nô là \(x\left( {x > 0,km/h} \right)\)
Đổi 15 phút = \(\dfrac{{15}}{{60}} = \dfrac{1}{4}\)h
*) Xuôi dòng:
Vận tốc của ca nô là \(x + 4\left( {km/h} \right) \Rightarrow \) Thời gian xuôi dòng của ca nô là \(\dfrac{{80}}{{x + 4}}(h)\)
*) Ngược dòng:
Vận tốc ngược dòng của ca nô là \(x - 4\left( {km/h} \right) \Rightarrow \) Thời gian ngược dòng của ca nô là \(\dfrac{{72}}{{x - 4}}(h)\)
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút nên ta có phương trình:
\(\begin{array}{l}\;\;\;\;\dfrac{{72}}{{x - 4}} - \dfrac{{80}}{{x + 4}} = \dfrac{1}{4}\\ \Leftrightarrow \dfrac{{288(x + 4) - 320(x - 4)}}{{(x - 4)(x + 4)}} = \dfrac{{{x^2} - 16}}{{(x - 4)(x + 4)}}\\ \Rightarrow - 32x + 2432 = {x^2} - 16\\ \Leftrightarrow {x^2} + 32x - 2448 = 0\\\Delta = {16^2} + 2448 = 2704 \Rightarrow \sqrt \Delta = 52\end{array}\)
Phương trình có hai nghiệm \(x = - 16 + 52 = 36(tmdk)\),\(x = - 16 - 52 = - 68\) (loại)
Vậy vận tốc thực của ca nô là \(36km/h.\)
Hướng dẫn giải:
Các bước giải bài toán bằng cách lập phương trình:
+) Chọn ẩn và đặt điều kiện cho ẩn
+) Biểu thị các đại lượng chưa biết qua ẩn và các đại lượng đã biết.
+) Lập phương trình-giải phương trình.
+) Chọn kết quả và trả lời.
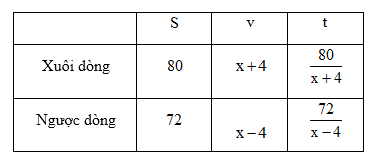
Phương trình: \(\dfrac{{72}}{{x - 4}} - \dfrac{{80}}{{x + 4}} = \dfrac{1}{4}\)

