Câu hỏi:
2 năm trước
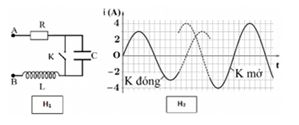
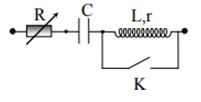
Đặt một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu một đoạn mạch như hình vẽ. Khi K đóng, điều chỉnh giá trị biến trở đến giá trị \({R_1}\) hoặc \({R_2}\) thì công suất tỏa nhiệt trên mạch đều bằng \(P\). Độ lệch pha giữa điện áp tức thời hai đầu mạch và dòng điện trong mạch khi \(R = {R_1}\) là \({\varphi _1}\), khi \(R = {R_2}\) là \({\varphi _2}\) , trong đó \(\left| {{\varphi _1} - {\varphi _2}} \right| = \frac{\pi }{6}\) . Khi K mở, điều chỉnh giá trị \(R\) từ \(0\) đến rất lớn thì công suất tỏa nhiệt trên biến trở \(R\) cực đại bằng \(\frac{{2P}}{3}\), công suất trên cả mạch cực đại bằng \(\frac{{2P}}{{\sqrt 3 }}\). Hệ số công suất của cuộn dây là:
Trả lời bởi giáo viên
Đáp án đúng: d
Khi K đóng, mạch chỉ có R, C mắc nối tiếp.
Khi \({R_1},{R_2}\) thì \({P_1} = {P_2}\) nên:
\(\begin{array}{*{20}{l}}{i = 0,5{I_0} = {I_0}.\cos {\varphi _{i2}} \Rightarrow {\varphi _{i2}} = \frac{\pi }{3} \Rightarrow \Delta {\varphi _m} = {\varphi _u} - {\varphi _{i1}} = \frac{{ - \pi }}{3}}\\\begin{array}{l} \Rightarrow \tan \Delta {\varphi _m} = \frac{{{Z_L} - {Z_C}}}{r} = - \sqrt 3 \Rightarrow {Z_L} - {Z_C} = - \sqrt 3 r\\ \Rightarrow {Z_L} - {Z_C} = - \sqrt 3 r = \frac{{ - 1}}{{\sqrt 3 }}(R + r) \Rightarrow R = 2r\end{array}\\{ \Rightarrow {Z_2} = \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} = 2r;{Z_1} = \sqrt {{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}} = 2\sqrt 3 r}\\{{I_{01}} = \frac{{{U_0}}}{{{Z_1}}};{I_{02}} = \frac{{{U_0}}}{{{Z_2}}} \Rightarrow \frac{{{I_{01}}}}{{{I_{02}}}} = \frac{{{Z_2}}}{{{Z_1}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {I_{02}} = {I_0} = 3A}\end{array}\)
Khi K mở thì mạch R, r, L, C nối tiếp Công suất mạch cực đại là:
\({P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2({R_0} + r)}} = \frac{2}{{\sqrt 3 }}P \Rightarrow {Z_L} = 2{Z_C}\)
Công suất trên R cực đại: \({P_{R\max }} = \frac{{{U^2}}}{{2R}} = \frac{{2P}}{3} \Leftrightarrow {R^2} = {r^2} + {({Z_L} - {Z_C})^2} \Rightarrow r = \frac{{{Z_C}}}{{\sqrt 3 }}\)
Thay các giá trị tìm được vào tính hệ số công suất cuộn dây: \(\cos {\varphi _d} = \frac{r}{{\sqrt {{r^2} + {Z_L}^2} }} = \frac{1}{{\sqrt {13} }}\)
Hướng dẫn giải:
Sử dụng biến đổi toán học và các điều kiện P cực trị
+ Sử dụng biểu thức định luật ôm: \(I = \frac{U}{R}\)
+ Sử dụng công thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
