Cho dòng điện xoay chiều chạy qua đoạn mạch AB có sơ đồ như hình bên, trong đó L là cuộn cảm thuần và X là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch AN và MB có biểu thức lần lượt \({u_{AN}} = 30\sqrt 2 cos\omega t(V);{u_{MB}} = 40\sqrt 2 cos\left( {\omega t - \frac{{\pi {\rm{}}}}{2}} \right)(V)\)
Điện áp hiệu dụng giữa hai đầu đoạn mạch AB có giá trị nhỏ nhất là:
![]()
Trả lời bởi giáo viên
\({u_{AN}} = {u_L} + {u_X}\)
\({u_{MB}} = {u_C} + {u_X}\)
\({u_{AB}} = {u_{AN}} + {u_C}\)
\({U_{AB}} \ge OH \to \left( {{U_{AB}}} \right)min = OH\)
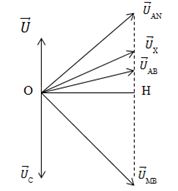
Áp dụng hệ thức lượng trong tam giác vuông ta có : \(\frac{1}{{U_{AB}^2}} = \frac{1}{{U_{AN}^2}} + \frac{1}{{U_{MB}^2}} \Rightarrow {U_{AB}} = 24V\)
Hướng dẫn giải:
Sử dụng giản đồ vecto và hệ thức lượng trong tam giác vuông