Câu hỏi:
2 năm trước
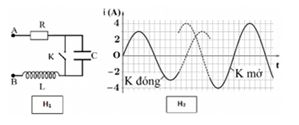
Đặt điện áp xoay chiều \(u = {U_0}cos\left( {\omega t + \varphi } \right)\) vào hai đầu đoạn mạch AB gồm điện trở , tụ điện và cuộn cảm thuần mắc nối tiếp (hình \({H_1}\) ). Ban đầu khóa K đóng, sau đó khóa K mở. Hình \({H_2}\) là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện i trong đoạn mạch vào thời gian t. Giá trị của \({U_0}\) gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
\(\begin{array}{l}\dfrac{{U_0^2}}{{{3^2}}} = R_0^2 + Z_L^2 \Rightarrow Z_L^2 = \dfrac{{U_0^2}}{{{3^2}}} - 5,76\\\dfrac{{U_0^2}}{{{4^2}}} = R_0^2 + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow {\left( {{Z_L} - {Z_C}} \right)^2} = \dfrac{{U_0^2}}{{{4^2}}} - 5,76{R^2} = {Z_L}\left( {{Z_L} - {Z_C}} \right)\\ \Rightarrow \dfrac{{{R^2}}}{{Z_L^2}} = \dfrac{{{Z_L} - {Z_C}}}{{{Z_L}}} \Rightarrow \dfrac{{\dfrac{{U_0^2}}{{{4^2}}} - 5,76}}{{\dfrac{{U_0^2}}{{{3^2}}} - 5,76}} = {\left( {\dfrac{{{R^2}}}{{Z_L^2}}} \right)^2}\end{array}\)
\(\begin{array}{l} \Rightarrow \left( {\dfrac{{U_0^2}}{{{4^2}}} - 5,76} \right)\left( {\dfrac{{U_0^2}}{{{3^2}}} - 5,76} \right) = {R^4}\left( {\dfrac{{U_0^2}}{{{3^2}}} - 5,76} \right)\\ \Rightarrow \left( {\dfrac{{U_0^2}}{{{4^2}}} - 5,76} \right)\left( {\dfrac{{U_0^2}}{{{3^2}}} - 5,76} \right) = {R^4} \Rightarrow \dfrac{{U_0^4}}{{{3^2}{{.4}^2}}} - 5,76\left( {\dfrac{{U_0^2}}{{{3^2}}} + \dfrac{{U_0^2}}{{{4^2}}}} \right) = 0\\ \Rightarrow {U_0} = R\sqrt {{3^2} + {4^2}} = 120V\end{array}\)
Hướng dẫn giải:
+ Sử dụng công thức
\({I_0} = \dfrac{{{U_0}}}{Z}\)
+ Sử dụng công thức tính độ lệch pha
\(tan\varphi = \dfrac{{\left( {{Z_L}-{\rm{ }}{Z_C}} \right)}}{R}\)
+ Kĩ năng đọc đồ thị
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
