Câu hỏi:
2 năm trước
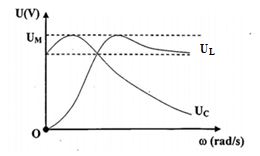
Đặt điện áp \(u = 200cos\omega t\left( V \right)\) (\(\omega \) thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm $L$, điện trở $R$ và tụ điện có điện dung $C$, với \(C{R^2} < 2L\). Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là \({U_C},{U_L}\) phụ thuộc vào \(\omega \), chúng được biểu diễn bằng các đồ thị như hình vẽ bên, tương ứng với các đường \({U_C},{U_L}\). Giá trị của \({U_M}\) trong đồ thị gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: a
Khi \(\omega {\rm{ }} = {\rm{ }}0\) thì \({U_C} = U\)
Khi \(\omega {\rm{}} = {\omega _C} = \sqrt {\dfrac{{2L - {R^2}C}}{{2{L^2}C}}} \)
thì \({U_C}\) cực đại
Khi \(\omega {\rm{}} = {\omega _R} = \sqrt {\dfrac{1}{{LC}}} \)
thì \({U_R}\) đạt cực đại bằng \(U\)
Khi \(\omega = 0\) thì \({U_L} = 0\) khi \(\omega {\rm{}} = {\omega _L} = \sqrt {\dfrac{2}{{2LC - {R^2}C}}} \)
thì \({U_{{L_{max}}}} = {U_M}\)
Đặt \(n = \dfrac{{{\omega _L}}}{{{\omega _C}}} = \dfrac{{2L}}{{2L - {R^2}C}} = {\rm{}} > \dfrac{1}{n} = 1 - \dfrac{{{R^2}C}}{{2L}} = 1 - \dfrac{{{R^2}}}{{2{Z_L}{Z_C}}};{\left( {\dfrac{U}{{{U_{{L_{max}}}}}}} \right)^2} + {\left( {\dfrac{1}{n}} \right)^2} = {\left( {\dfrac{U}{{{U_{{C_{max}}}}}}} \right)^2} + {\left( {\dfrac{1}{n}} \right)^2} = 1\)
Tại giao điểm của hai đồ thị, ta có \({U_L} = {U_C} = U\) (cộng hưởng )
\(\begin{array}{*{20}{l}}
{ = {\text{}} > \dfrac{1}{n} = 1 - \dfrac{{{R^2}}}{{2{Z_L}{Z_C}}} = 1 - \dfrac{{U_R^2}}{{2{U_L}{U_C}}} = 1 - \dfrac{{{U^2}}}{{2.U.U}} = \dfrac{1}{2} = {\text{}} > n = 2} \\
{{U_M} = {U_{{C_{max}}}} = {U_{{L_{max}}}} = \dfrac{{nU}}{{\sqrt {{n^2} - 1} }} = \dfrac{{2.100\sqrt 2 }}{{\sqrt {{2^2} - 1} }} = 163,3(V)}
\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức \(\omega \) biến thiên để \({U_{Cm{\rm{ax}}}}\), khi đó: \({\omega _C} = \sqrt {\dfrac{{2L - {R^2}C}}{{2{L^2}C}}} \)
+ \(\omega = \dfrac{1}{{\sqrt {LC} }}\) : mạch cộng hưởng \({U_{Rm{\rm{ax}}}}\)
+ \(\omega \) biến thiên để \({U_{L\max }}\), khi đó: \({\omega _L} = \sqrt {\dfrac{2}{{2LC - {R^2}C}}} \)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
