Câu hỏi:
2 năm trước
Cho tứ diện đều ABCD có cạnh bằng 2a. Khoảng cách giữa hai đường thẳng AB và CD là
Trả lời bởi giáo viên
Đáp án đúng: b
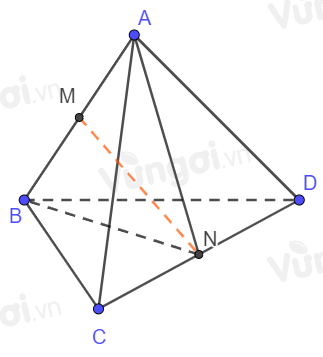
Bước 1: Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh MN là đoạn vuông góc chung của AB và CD.
Gọi M, N lần lượt là trung điểm của AB và CD.
\(\Delta BCD,\Delta ACD\) đều nên:
\(\left. \begin{array}{l}AN \bot CD\\BN \bot CD\end{array} \right\} \Rightarrow \left( {ABN} \right) \bot CD \Rightarrow MN \bot CD\)
Tương tự ta có \(MN \bot AB\)
Khoảng cách giữa 2 đường thẳng AB, CD là độ dài của MN.
Bước 2: Tính MN.
\(\Delta ACD\) đều cạnh 2a; AN là đường cao.
\( \to AN = AC.\dfrac{{\sqrt 3 }}{2} = 2a.\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)
\(AM = \dfrac{1}{2}AB = a\)
\(\Delta AMN\) vuông tại M (\(MN \bot AB\)) nên:
\(MN = \sqrt {A{N^2} - A{M^2}} \) \( = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
Hướng dẫn giải:
Bước 1: Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh MN là đoạn vuông góc chung của AB và CD.
Bước 2: Tính MN.
