Câu hỏi:
2 năm trước
Cho tam giác $A B C$ vuông tại \(A\). Mặt phẳng \((P)\) chứa $B C$ và hợp với mặt phẳng \((ABC)\) góc \(\alpha \left( {{0^0} < \alpha < {{90}^0 }} \right)\). Gọi \(\beta ,\gamma \) lần lượt là góc hợp bởi hai đường thẳng $A B, A C$ và \((P)\). Tính giá trị biểu thức \(p = {\cos ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma \).
Trả lời bởi giáo viên
Đáp án đúng:
\(P = 1\).
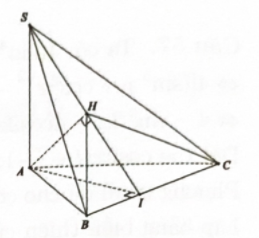
Gọi \(d\) là đường thẳng vuông góc với \((ABC)\) tại $A$, $S$ là giao điểm của \(d\) với \((P)\). Khi đó \((P)\) chính là \((SBC)\).
Kẻ \(AI \bot BC(I \in BC),AH \bot SI(H \in SI)\).
Khi đó \(\alpha = \widehat {SIA};\beta = \widehat {ABH};\gamma = \widehat {ACH}\).
\(\begin{array}{l}p = {\cos ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma \\ = \dfrac{{H{I^2}}}{{A{I^2}}} + \dfrac{{A{H^2}}}{{A{B^2}}} + \dfrac{{A{H^2}}}{{A{C^2}}}\end{array}\)
\(\begin{array}{l} = \dfrac{{H{I^2}}}{{A{I^2}}} + A{H^2}\left( {\dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}} \right)\\ = \dfrac{{H{I^2}}}{{A{I^2}}} + \dfrac{{A{H^2}}}{{A{I^2}}} = 1.\end{array}\)
Hướng dẫn giải:
Bước 1: Gọi \(d\) là đường thẳng vuông góc với \((ABC)\) tại $A$, $S$ là giao điểm của \(d\) với \((P)\). Kẻ \(AI \bot BC(I \in BC),AH \bot SI(H \in SI)\)
Bước 2: Tính \(p = {\cos ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma \)
