Câu hỏi:
2 năm trước
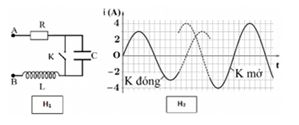
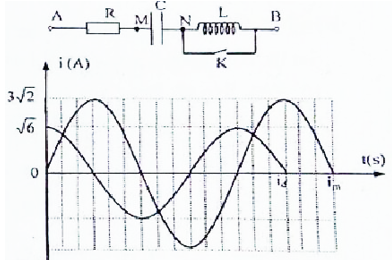
Cho mạch điện như hình vẽ, cuộn dây thuần cảm. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = 100\sqrt 6 \cos \left( {100\pi t + \varphi } \right)V\). Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là \({i_m}\) và \({i_d}\) được biểu diễn như hình bên. Điện trở các dây nối rất nhỏ. Giá trị của \(R\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
Từ đồ thị ta thấy được biểu thức của cường độ dòng điện khi K đóng và mở là: \(\left\{ \begin{array}{l}{i_m} = 3\sqrt 2 \cos \left( {\omega t + \frac{\pi }{2}} \right)A\\{i_d} = \sqrt 6 \cos \left( {\omega t} \right)A\end{array} \right.\)
+ Khi khóa K đóng, mạch điện chỉ gồm R mắc nối tiếp với C
Tổng trở được tính theo công thức: \({Z_{RC}} = \sqrt {{R^2} + Z_C^2} {\rm{}} = \dfrac{{{U_0}}}{{{I_{01}}}} = \dfrac{{100\sqrt 6 }}{{\sqrt 6 }} = 100\Omega (1)\)
+ Khi khóa K mở, mạch điện gồm ba phần tử R, L, C mắc nối tiếp. Tổng trở được tính theo công thức \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = \dfrac{{{U_0}}}{{{I_{0m}}}} = \dfrac{{100\sqrt 6 }}{{3\sqrt 2 }} = \dfrac{{100\sqrt 3 }}{3}\Omega (2)\)
+ Từ biểu thức cường độ \({i_m}\) và \({i_d}\) ta thấy rằng hai dòng điện vuông pha với nhau, khi đó ta có: \(\dfrac{{{Z_C}}}{R}.\dfrac{{{Z_L} - {Z_C}}}{R} = 1 \Leftrightarrow {R^2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)\left( 3 \right)\)
Thay (3) vào (1) và (2) ta được
\(\left\{ {\begin{array}{*{20}{l}}
{{Z_C}\left( {{Z_L} - {Z_C}} \right) + Z_C^2 = {{100}^2}} \\
{{Z_C}\left( {{Z_L} - {Z_C}} \right) + {{\left( {{Z_L} - {Z_C}} \right)}^2} = \dfrac{{{{100}^2}.3}}{9}}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{Z_L} = \dfrac{{200}}{{\sqrt 3 }}\Omega } \\
{{Z_C} = 50\sqrt 3 \Omega {\text{}}}
\end{array}} \right.\)
Thay vào (3) suy ra: \(R = 50\Omega \)
Hướng dẫn giải:
Sử dụng kĩ năng đọc đồ thị và lí thuyết về đoạn mạch xoay chiều mắc nối tiếp
+ Từ đồ thị => viết phương trình cường độ dòng điện trong hai trường hợp: đóng và mở khóa K
+ Sử dụng công thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \frac{U}{I}\)
+ \({\varphi _1} + {\varphi _2} = \frac{\pi }{2} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\)
+ Sử dụng biểu thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
