Câu hỏi:
2 năm trước
Cho hình thang $ABCD$ (\(AB\,{\rm{//}}\,CD\)) có \(\widehat {ADB} = \widehat {BCD}\), $AB = 2cm$ , \(BD = \sqrt 5 \,cm\), ta có:
Trả lời bởi giáo viên
Đáp án đúng: d
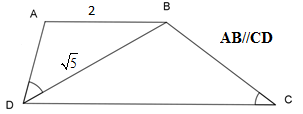
Vì \(AB\,{\rm{//}}\,CD\) nên: \(\widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(\Delta ADB\) và \(\Delta BCD\) ta có:
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
\(\widehat {ADB} = \widehat {BCD}\) (theo gt)
\( \Rightarrow \Delta ADB\backsim\Delta BCD\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{DB}}{{CD}}\)\( \Leftrightarrow \dfrac{2}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{{CD}} \)\(\Leftrightarrow CD = \dfrac{{\sqrt 5 .\sqrt 5 }}{2} = \dfrac{5}{2} = 2,5\;cm\)
Hướng dẫn giải:
- Chứng minh $2$ tam giác đồng dạng theo trường hợp góc – góc.
- Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra độ dài đoạn thẳng $CD$ .
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
