Câu hỏi:
2 năm trước
Cho hình bình hành $ABCD$ , điểm $F$ trên cạnh $BC$ . Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G$ . Chọn khẳng định sai.
Trả lời bởi giáo viên
Đáp án đúng: c
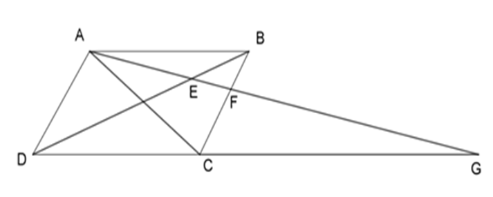
Có ABCD là hình bình hành nên:
\(AD{\rm{//}}BC,\;AB{\rm{//}}\,DC\)
\( \Rightarrow \widehat {ADE} = \widehat {FBE}\)(cặp góc so le trong)
\( \Rightarrow \widehat {ABE} = \widehat {EDG}\)(cặp góc so le trong)
Xét tam giác $BFE$ và tam giác $DAE$ có:
\(\widehat {ADE} = \widehat {FBE}\;(cmt)\)
\(\widehat {AED} = \widehat {FEB}\)(đối đỉnh)
\( \Rightarrow \Delta BFE\backsim\Delta DAE\;(g - g)\)nên A đúng, C sai.
Xét tam giác $DGE$ và tam giác $BAE$ có:
\(\widehat {ABE} = \widehat {EDG\;}(cmt)\)
\(\widehat {AEB} = \widehat {GED}\)(đối đỉnh)
\( \Rightarrow \Delta DGE\backsim\Delta BAE\;(g - g)\)hay \(\Delta DEG\backsim\Delta BEA\) nên B, D đúng.
Hướng dẫn giải:
- Tìm dữ kiện cần để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
