Câu hỏi:
2 năm trước
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Với giá trị nào của tham số \(m\) thì phương trình \(\left| {f\left( x \right) - 1} \right| = m\) có bốn nghiệm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: b
Dựa vào bảng biến thiên của hàm số \(y = f\left( x \right)\), ta có bảng biến thiên của hàm số \(y = f\left( x \right) - 1\) là:
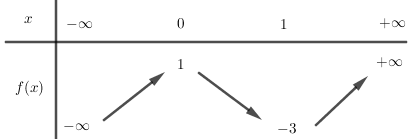
Suy ra bảng biến thiên của hàm số \(y = \left| {f\left( x \right) - 1} \right|\)
Từ BBT suy ra phương trình \(\left| {f\left( x \right) - 1} \right| = m\) có bốn nghiệm phân biệt khi \(1 < m < 3\).
Vậy \(1 < m < 3\).
Hướng dẫn giải:
Lập bảng biến thiên của hàm số \(y = \left| {f\left( x \right) - 1} \right|\) với chú ý:
+ Đồ thị hàm số \(y = f\left( x \right) - 1\) có được từ việc tịnh tiến \(y = f\left( x \right)\) xuống dưới \(1\) đơn vị.
+ Đồ thị hàm số \(y = \left| {f\left( x \right)}-1 \right|\) có được từ việc giữ nguyên phần đồ thị \(y = f\left( x \right)-1\) phía trên trục hoành và lấy đối xứng phần dưới qua trục hoành, đồng thời xóa bỏ phần dưới cũ.
