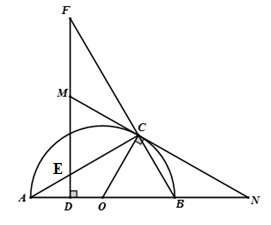
Cho điểm \(C\) thuộc nửa đường tròn \(\left( O \right)\) đường kính \(AB.\) Từ điểm \(D\) thuộc đọan \(AO\) kẻ đường thẳng vuông góc với \(AO\) cắt \(AC\) và \(BC\) lần lượt lại \(E\) và \(F.\) Tiếp tuyến tại \(C\) với nửa đường tròn cắt $EF$ tại \(M\) và cắt \(AB\) tại \(N.\) Khi đó
Trả lời bởi giáo viên
Ta có \(\widehat {MCA} = \dfrac{1}{2}\) sđ \(\overparen{AC}\) (góc giữa tiếp tuyến và dây cung chắn cung \(AC\)) \(\left( 1 \right).\)
Lại có \(\widehat {MEC} = \widehat {AED} = {90^0} - \widehat {EAD} = {90^0} - \dfrac{1}{2}\) sđ \(\overparen{BC} = \dfrac{1}{2}\) sđ \(\overparen{AC}\,\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {MCE} = \widehat {MEC}.\)
Vậy \(\Delta MEC\) cân tại \(M,\) suy ra \(MC = ME.\)
Chứng minh tương tự ta có \(MC = MF.\)
Suy ra \(ME = MF.\)


