Trả lời bởi giáo viên
Đáp án đúng: c
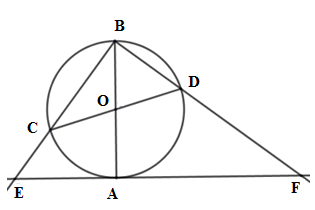
Xét (O) có AB;CD là các đường kính nên ^CBD=90∘
Xét tam giác BCD vuông tại B có ^BCD+^BDC=90∘ mà ^OBD=^ODB (do ΔOBD cân tại O )
Nên ^BCD+^OBD=90∘⇒^BCD=90∘−^OBD (1)
Xét tam giác ABF vuông tại A (vì EF là tiếp tuyến của (O)) có ^BFA=90∘−^ABF (2)
Từ (1) và (2) suy ra ^BCD=^DFA
Do đó tứ giác DCEF là tứ giác nội tiếp (dấu hiệu góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó là tứ giác nội tiếp.


