Trả lời bởi giáo viên
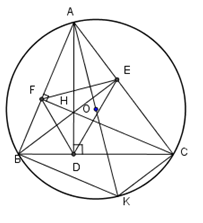
Theo giả thiết ta có \(CF,\,BE\) là các đường cao của tam giác \(ABC\)
nên \(CF \bot AB,\,BE \bot AC.\) Do đó \(\widehat {BFC} = {90^0},\,\widehat {BEC} = {90^0}.\)
Theo dấu hiệu nhận biết tứ giác nội tiếp ta suy ra \(BFEC\) là tứ giác nội tiếp nên C đúng.
\( \Rightarrow \widehat {AFE} = \widehat {ACB}\) (cùng bù với \(\widehat {BFE}\))
Xét hai tam giác $AEF$ và \(ABC\) có \(\widehat A\) chung; \(\widehat {AFE} = \widehat {ACB}\left( {cmt} \right) \Rightarrow \Delta AEF \backsim \Delta ABC\left( {g.g} \right)\) nên B đúng.
Lại có \(\widehat {HEC} + \widehat {HDC} = {90^0} + {90^0} = {180^0}\) nên tứ giác \(CDHE\) là tứ giác nội tiếp nên D đúng.
Hướng dẫn giải:
Sử dụng các dấu hiệu nhận biết tứ giác nội tiếp:
- Tổng hai góc đối bằng \({180^0}\).
- Hai đỉnh kề nhau cùng nhìn về cạnh đối diện các góc bằng nhau.
- Sử dụng trường hợp đồng dạng góc – góc để chứng minh các tam giác đồng dạng.


