Trả lời bởi giáo viên
Đáp án đúng: c
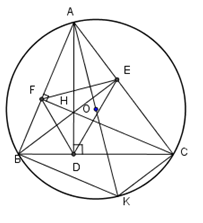
Theo giả thiết ta có CF là đường cao của ΔABC nên AF⊥CF(1). Mặt khác AK là đường kính của (O) nên theo tính chất của góc nội tiếp chắn nửa đường tròn ta suy ra ^ABK=900⇒BK⊥AB(2).
Từ (1),(2) suy ra HC//BK(3).
Chứng minh tương tự ta có BH//CK(4).
Từ (3),(4) ta nhận được BHCK là hình bình hành.
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp chắn nửa tròn để chứng minh ^ABK=^ACK=900.
Sử dụng định lý từ vuông góc đến song song để chứng minh BK//CF;CK//BE.
Sử dụng dấu hiệu nhận biết các hình đặc biệt.


