Cho $\Delta ABC$ có các đường cao $BD$ và $CE$ cắt nhau tại $H.$ Gọi $M$ là giao của $AH$ với $BC.$

Chọn khẳng định sai.

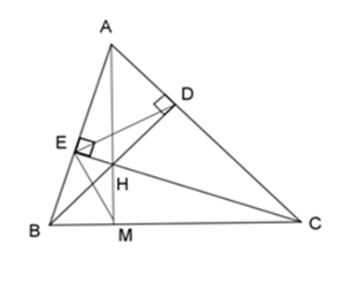
Theo cmt ta có: \(\Delta HBE\backsim\Delta HCD\)

\( \Rightarrow \dfrac{{HE}}{{HD}} = \dfrac{{HB}}{{HC}} \Leftrightarrow \dfrac{{HE}}{{HB}} = \dfrac{{HD}}{{HC}}\)

Xét \(\Delta HED\) và \(\Delta HBC\) ta có:

   \(\dfrac{{HE}}{{HB}} = \dfrac{{HD}}{{HC}}\) (chứng minh trên)

   \(\widehat {EHD} = \widehat {BHC}\) (2 góc đối đỉnh)

   \(\begin{array}{l}\widehat {HDE} = \widehat {HAE}\\ \Rightarrow \Delta HED\backsim\Delta HBC\,\,\,\left( {c - g - c} \right).\\ \Rightarrow \widehat {HDE} = \widehat {HCB}\,\,\,\,\,\left( 1 \right)\end{array}\)

Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)

\( \Rightarrow \) H là trực tâm của \(\Delta ABC\).

\( \Rightarrow AH \bot BC\) tại M \( \Rightarrow \widehat {AMB} = {90^0}\).

Xét \(\Delta AMB\) và \(\Delta CEB\) có:

   \(\widehat {CEB} = \widehat {AMB} = {90^0}\)

   \(\widehat B\) chung

\( \Rightarrow \Delta AMB\backsim\Delta CEB\;(g - g)\)

\( \Rightarrow \widehat {MAB} = \widehat {ECB}\;hay\;\widehat {HAE} = \widehat {HCB}\;(2)\)

Từ (1) và (2) ta có: \(\widehat {HDE} = \widehat {HAE}\)  nên A, B, C đúng. D sai.