Câu hỏi:
2 năm trước
Cho $\Delta ABC$ có các đường cao $BD$ và $CE$ cắt nhau tại $H.$ Gọi $M$ là giao của $AH$ với $BC.$
Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
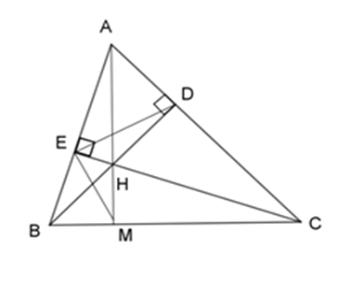
Xét \(\Delta HBE\) và \(\Delta HCD\) có:
\(\widehat {BDC} = \widehat {CEB} = {90^0}\)
\(\widehat {EHB} = \widehat {DHC}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta HBE\backsim\Delta HCD\)(g – g)
Xét \(\Delta ABD\) và \(\Delta ACE\) có
\(\widehat {AEC} = \widehat {BDA} = 90^\circ \)
\(\widehat A\) chung
Nên \(\Delta ABD\backsim\Delta ACE\,\left( {g - g} \right)\).
Hướng dẫn giải:
Chứng minh hai tam giác đồng dạng theo trường hợp góc-góc.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
