Câu hỏi:
2 năm trước
Cho \(BC\) là một dây cung của đường tròn \(\left( {O;R} \right),\,\,\left( {BC \ne 2R} \right).\) Điểm \(A\) di động trên cung lớn \(BC\) sao cho \(O\) luôn nằm trong tam giác \(ABC.\) Các đường cao \(AD,\,BE,\,CF\) của tam giác \(ABC\) đồng quy tại \(H.\)
Kẻ đường kính \(AK\) của đường tròn \(\left( {O;R} \right).\) Khi đó \(BHCK\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
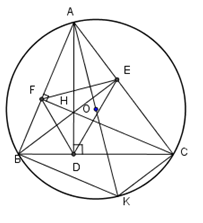
Theo giả thiết ta có \(CF\) là đường cao của \(\Delta ABC\) nên $AF \bot CF\,\left( 1 \right).$ Mặt khác \(AK\) là đường kính của \(\left( O \right)\) nên theo tính chất của góc nội tiếp chắn nửa đường tròn ta suy ra $\widehat {ABK} = {90^0} \Rightarrow BK \bot AB\,\,\left( 2 \right).$
Từ \(\left( 1 \right),\,\left( 2 \right)\) suy ra \(HC//BK\,\,\left( 3 \right).\)
Chứng minh tương tự ta có \(BH//CK\,\,\left( 4 \right).\)
Từ \(\left( 3 \right),\,\left( 4 \right)\) ta nhận được \(BHCK\) là hình bình hành.
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp chắn nửa tròn để chứng minh \(\widehat {ABK} = \widehat {ACK} = {90^0}\).
Sử dụng định lý từ vuông góc đến song song để chứng minh \(BK//CF;CK//BE\).
Sử dụng dấu hiệu nhận biết các hình đặc biệt.
