Câu hỏi:
2 năm trước
Cho 3 điểm A, B, C không thẳng hàng. Gọi D là trung điểm của AC, quỹ tích điểm M thỏa mãn \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\) là
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có
\(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\)
\( \Leftrightarrow \left| {2\overrightarrow {MD} + 2\overrightarrow {MB} } \right| = \left| {\overrightarrow {BA} } \right|\)(1)
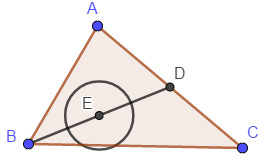
Gọi E là trung điểm của BD. Khi đó:
(1)\( \Leftrightarrow 4\left| {\overrightarrow {ME} } \right| = AB \Leftrightarrow ME = \dfrac{1}{4}AB\).
Vậy quỹ tích của M là đường tròn tâm E bán kính \(\dfrac{1}{4}AB\).
Hướng dẫn giải:
Hiệu hai vec tơ: \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} \)
Tính chất trung điểm: D là trung điểm của AC nên \(2\overrightarrow {MD} = \overrightarrow {MA} + \overrightarrow {MC} \).
\(\overrightarrow {MA} + 2\overrightarrow {MB} + \overrightarrow {MC} = 2\left( {\overrightarrow {MD} + \overrightarrow {MB} } \right)\) nên ta lấy E là trung điểm của BD. Biểu diễn \(\overrightarrow {MA} + 2\overrightarrow {MB} + \overrightarrow {MC} \) theo \(\overrightarrow {ME} \).
