Công thức liên hệ công suất của dòng điện, cường độ dòng điện, trên một đoạn mạch giữa hai đầu có hiệu điện thế U là:
Công suất điện trong một đoạn mạch bằng tích hiệu điện thế giữa hai đầu đoạn mạch với cường độ dòng điện qua nó.
Công thức: \(P = UI\)
Một bếp điện có điện trở R được mắc vào hiệu điện thế U thì dòng điện qua nó có cường độ I. Khi đó công suất của bếp là P. Biểu thức nào sau đây xác định P không đúng?
Ta có công suất của bếp: \(P = UI\)
Mặt khác: \(I = \frac{U}{R}\)
Ta suy ra: \(P = UI = \frac{{{U^2}}}{R} = {I^2}R\)
Có hai điện trở \({R_1}\) và \({R_2} = 2{{\rm{R}}_1}\) được mắc song song vào một hiệu điện thế không đổi. Công suất điện \({P_1},{P_2}\) tương ứng trên hai điện trở này có mối quan hệ nào dưới đây?
+ Vì hai điện trở \({{\rm{R}}_1}\) và \({R_2}\) được mắc song song vào một hiệu điện thế không đổi \(U\), nên ta có:
\(U = {U_1} = {U_2}\)
+ Công suất trên hai điện trở: \(\left\{ \begin{array}{l}{P_1} = \frac{{U_1^2}}{{{R_1}}} = \frac{{{U^2}}}{{{R_1}}}\\{P_2} = \frac{{U_2^2}}{{{R_2}}} = \frac{{{U^2}}}{{{R_2}}}\end{array} \right.\)
Từ đây, ta suy ra: \(\frac{{{P_1}}}{{{P_2}}} = \frac{{{R_2}}}{{{R_1}}} = 2 \to {P_1} = 2{P_2}\)
Trên nhiều dụng cụ điện trong gia đình thường có ghi 220V và số oát (W). Số oát này có ý nghĩa gì?
Số oát trên dụng cụ tiêu thụ điện có ý nghĩa công suất tiêu thụ điện của dụng cụ khi nó được sử dụng đúng với hiệu điện thế 220V
Trên bóng đèn có ghi \(6V-3W\). Khi đèn sáng bình thường thì dòng điện chạy qua đèn có cường độ là:
Ta có:
+ Số chỉ trên bóng đèn cho biết hiệu điện thế định mức và công suất định mức: \(U = 6V,P = 3{\rm{W}}\)
+ Khi đèn sáng bình thường thì dòng điện chạy qua đèn có giá trị: \(I = \dfrac{P}{U} = \dfrac{3}{6} = 0,5{\rm{A}}\)
Một bóng đèn có ghi \(\left( {220V - 60W} \right)\) mắc vào một nguồn điện. Khi đó cường độ dòng điện qua đèn là \(0,18A\) thì ta thấy đèn sáng:
Ta có:
+ Số chỉ trên bóng đèn cho biết hiệu điện thế định mức và công suất định mức: \(U = 220V,P = 60{\rm{W}}\)
+ Khi đèn sáng bình thường thì dòng điện chạy qua đèn có giá trị: \(I = \dfrac{P}{U} = \dfrac{{60}}{{220}} = 0,273{\rm{A}}\)
=> Khi cường độ dòng điện qua đèn là $0,18A < I$
=> Đèn sáng yếu hơn bình thường.
Bóng đèn ghi 12V- 100W. Tính điện trở của đèn
Ta có:
+ \(U = 12V,P = 100{\rm{W}}\)
+ Áp dụng biểu thức: \(P = \frac{{{U^2}}}{R} \to R = \frac{{{U^2}}}{P} = \frac{{{{12}^2}}}{{100}} = 1,44\Omega \)
Bóng đèn có điện trở \(8\Omega \) và cường độ dòng điện định mức là \(2A\). Tính công suất định mức của bóng đèn?
Công suất định mức của bóng đèn: \(P = {I^2}R = {2^2}.8 = 32W\)
Bóng đèn có điện trở \(9\Omega \) và hiệu điện thế qua nó là \(24V\) thì nó sáng bình thường. Tính công suất định mức của bóng đèn?
Công suất định mức của bóng đèn: \(P = UI = \frac{{{U^2}}}{R} = \frac{{{{24}^2}}}{9} = 64{\rm{W}}\)
Ở công trường xây dựng có sử dụng một máy nâng, để nâng khối vật liệu có trọng lượng \(2000N\) lên tới độ cao \(15m\) trong thời gian \(40\) giây. Phải dùng động cơ điện có công suất nào dưới đây là thích hợp cho máy nâng này nếu tính cả công suất hao phí?
Ta có:
+ Công suất có ích để nâng vật là: \(P = \frac{A}{t} = \frac{{P.h}}{t} = \frac{{2000.15}}{{40}} = 750W\)
Nếu bỏ qua công suất hao phí, để nâng được vật trên thì phải dùng động cơ điện có công suất:
\(P \ge 750W\)
Ta suy ra, công suất thích hợp cho máy nâng từ các đáp án là: \(P = 0,8k{\rm{W}} = 800{\rm{W}}\)
Trên bóng đèn Đ1, Đ2 có ghi số tương ứng là \(3V - 1,2W\) và \(6V - 6W\). Cần mắc hai đèn này cùng với một biến trở vào hiệu hiệu điện thế \(U = 9V\)để hai đèn sáng bình thường.
Cần mắc hai đèn và biến trở như thế nào để thỏa mãn yêu cầu của đề bài?
+ Vì \({U_1} + {U_2} = 3 + 6 = 9V\) nên hai đèn Đ1 và Đ2 phải mắc nối tiếp nhau
+ Cường độ dòng điện định mức để mỗi đèn sáng bình thường là: \(\left\{ \begin{array}{l}{I_1} = \dfrac{{{P_1}}}{{{U_1}}} = \dfrac{{1,2}}{3} = 0,4{\rm{A}}\\{I_2} = \dfrac{{{P_2}}}{{{U_2}}} = \dfrac{6}{6} = 1{\rm{A}}\end{array} \right.\)
Vì \({I_2} > {I_1}\) nên để hai đèn sáng bình thường phải mắc biến trở \({R_b}\) song song với đèn Đ1 sao cho: \({I_2} = {I_1} + {I_b}\)
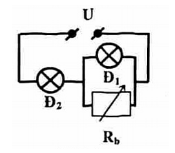
Trên bóng đèn Đ1, Đ2 có ghi số tương ứng là \(3V - 1,2W\) và \(6V - 6W\). Cần mắc hai đèn này cùng với một biến trở vào hiệu hiệu điện thế \(U = 9V\)để hai đèn sáng bình thường.
Công suất của biến trở khi đó có giá trị:
Ta có:
\({I_2} = {I_1} + {I_b} \to {I_b} = {I_2} - {I_1} = 1 - 0,4 = 0,6{\rm{A}}\)
Hiệu điện thế trên biến trở: \({U_b} = {U_1} = 3V\)
Công suất biến trở khi đó: \({P_b} = {U_b}{I_b} = 3.0,6 = 1,8W\)
Trên bóng đèn dây tóc Đ1 có ghi \(\left( {220V - 100W} \right)\), trên bóng đèn Đ2 có ghi \(\left( {220V - 75W} \right)\). Mắc hai bóng đèn trên nối tiếp nhau rồi mắc đoạn mạch này vào hiệu điện thế \(220V\). Tính công suất điện của đoạn mạch nối tiếp này, cho rằng điện trở của mỗi đèn khi đó bằng 50% điện trở của đèn đó khi sáng bình thường.
Ta có: Đ1 mắc nối tiếp Đ2
+ Cường độ dòng điện định mức trên mỗi đèn:
\(\left\{ \begin{array}{l}{I_1} = \dfrac{{{P_1}}}{{{U_1}}} = \dfrac{{100}}{{220}} = \dfrac{5}{{11}}A\\{I_2} = \dfrac{{{P_2}}}{{{U_2}}} = \dfrac{{75}}{{220}} = \dfrac{{15}}{{44}}A\end{array} \right.\)
Điện trở định mức của mỗi đèn: \(\left\{ \begin{array}{l}{R_1} = \dfrac{{{U_1}}}{{{I_1}}} = \dfrac{{220}}{{\dfrac{5}{{11}}}} = 484\Omega \\{R_2} = \dfrac{{{U_2}}}{{{I_2}}} = \dfrac{{220}}{{\dfrac{{15}}{{44}}}} = 645,33\Omega \end{array} \right.\)
+ Theo đề bài: \(\left\{ \begin{array}{l}{R_1}' = 50\% {R_1} = 242\Omega \\{R_2}' = 50\% {R_2} = 322,67\Omega \end{array} \right.\)
+ Điện trở tương đương của mạch nối tiếp khi đó: \({R_{nt}} = {R_1}' + {R_2}' = 564,67\Omega \)
Cách 1:
+ Cường độ dòng điện trong mạch nối tiếp: \(I = \dfrac{U}{{{R_{nt}}}} = \dfrac{{220}}{{564,67}} = 0,3896{\rm{A}}\)
Công suất điện của đoạn mạch nối tiếp này là:
\({P_{nt}} = UI = 220.0,3896 = 85,712W\)
Cách 2:
Công suất điện của đoạn mạch: \(P = \dfrac{{{U^2}}}{{{R_{nt}}}} = \dfrac{{{{220}^2}}}{{564,67}} \approx 85,71W\)
Trên hai bóng đèn có ghi \(220V - 60W\) và \(220V - 75W\). Biết rằng dây tóc của hai bóng đèn này đều bằng vônfram và có tiết diện bằng nhau. Dây tóc của đèn nào có độ dài lớn hơn và lớn hơn bao nhiêu lần?
Ta có: \(R = \rho \frac{l}{S}\) cho nên khi hai dây tóc làm cùng bằng một chất và có tiết diện bằng nhau thì dây nào có điện trở lớn hơn thì sẽ dài hơn.
Mặt khác, \(P = \frac{{{U^2}}}{R}\) cho nên khi hai bóng đèn có cùng hiệu điện thế định mức thì đèn nào có công suất lớn hơn sẽ có điện trở nhỏ hơn.
Vì vậy, đèn 2 sẽ có điện trở nhỏ hơn, do đó, dây tóc của đèn 1 sẽ dài hơn dây tóc của đèn 2.
Ta có:
\(\begin{array}{l}\frac{{{R_1}}}{{{R_2}}} = \frac{{\rho \frac{{{l_1}}}{S}}}{{\rho \frac{{{l_2}}}{S}}} = \frac{{{l_1}}}{{{l_2}}} = \frac{{\frac{{U_1^2}}{{{P_1}}}}}{{\frac{{U_2^2}}{{{P_2}}}}} = \frac{{{P_2}}}{{{P_1}}} = \frac{{75}}{{60}} = 1,25\\ \to {l_1} = 1,25{l_2}\end{array}\)
Một bóng đèn \(6V - 3W\) được mắc vào nguồn có hiệu điện thế \(6V\) nhờ dây dẫn dài \(2m\), tiết diện \(1m{m^2}\) và làm bằng chất có điện trở suất là \(0,{5.10^{ - 6}}\Omega .m\)
Đèn có sáng bình thường không?
+ Từ các thông số của đèn, ta có:
\(\left\{ \begin{array}{l}{U_D} = 6V\\{P_D} = 3W\end{array} \right.\)
Ta có điện trở của đèn: \({R_D} = \dfrac{{U_D^2}}{{{P_D}}} = \dfrac{{{6^2}}}{3} = 12\Omega \)
Cường độ dòng điện định mức của đèn: \({I_D} = \dfrac{{{P_D}}}{{{U_D}}} = \dfrac{3}{6} = 0,5A\)
+ Điện trở của dây nối: \(R = \rho \dfrac{l}{S} = 0,{5.10^{ - 6}}\dfrac{2}{{{{10}^{ - 6}}}} = 1\Omega \)
+ Điện trở tương đương của mạch: \({R_{t{\rm{d}}}} = {R_D} + R = 12 + 1 = 13\Omega \)
+ Cường độ dòng điện trong mạch: \(I = \dfrac{U}{{{R_{t{\rm{d}}}}}} = \dfrac{6}{{13}} = 0,46{\rm{A}}\)
Nhận thấy: \(I < {I_D}\) => đèn sáng yếu hơn bình thường
Một bóng đèn \(6V - 3W\) được mắc vào nguồn có hiệu điện thế \(6V\) nhờ dây dẫn dài \(2m\), tiết diện \(1m{m^2}\) và làm bằng chất có điện trở suất là \(0,{5.10^{ - 6}}\Omega .m\)
Công suất thực của đèn có giá trị là?
Ta có: Cường độ dòng điện qua mạch: \(I = 0,46{\rm{A}}\) tính ở câu trên
=> Công suất thực của đèn: \(P = {I^2}{R_D} = 0,{46^2}.12 = 2,54W\)
Một bàn là điện có công suất định mức 1100W và cường độ dòng điện định mức 5A. điện trở suất là 1,1.10-6Wm và tiết diện của dây là 0,5mm2, chiều dài của dây là :
Điện trở của bàn là: \(R = \dfrac{{{P_{dm}}}}{{I_{dm}^2}} = \dfrac{{1100}}{{{5^2}}} = 44\Omega \)
Chiều dài của dây là: \(l = \dfrac{{R.S}}{\rho } = \dfrac{{44.0,{{5.10}^{ - 6}}}}{{1,{{1.10}^{ - 6}}}} = 20m\)
Hai điện trở R1 = 10Ω và R2 = 30Ω mắc nối tiếp vào hiệu điện thế U = 12V. Công suất tiêu thụ của mỗi điện trở sẽ có giá trị nào sau đây?
Ta có: \(I = {I_1} = {I_2} = \dfrac{U}{{{R_{td}}}} = \dfrac{{12}}{{10 + 30}} = 0,3A\)
Công suất tiêu thụ: \(\left\{ \begin{array}{l}{P_1} = I_1^2{R_1} = 0,{3^2}.10 = 0,9W\\{P_2} = I_2^2{R_2} = 0,{3^2}.30 = 2,7W\end{array} \right.\)
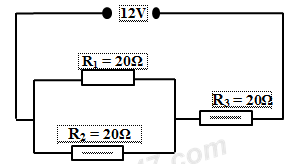
Có 3 điện trở giống nhau có giá trị bằng 20W được mắc như sơ đồ. Công suất tiêu thụ của cả đoạn mạch là:
Cách giải:
Mạch điện gồm: (R1 // R2) nt R3
Ta có:
\(\begin{array}{l}{R_{12}} = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = \frac{{20.20}}{{20 + 20}} = 10\Omega \\{R_{td}} = {R_{12}} + {R_3} = 10 + 20 = 30\Omega \\ \Rightarrow I = \frac{U}{{{R_{td}}}} = \frac{{12}}{{30}} = 0,4A\\ \Rightarrow P = U.I = 12.0,4 = 4,8W\end{array}\)
Một quạt điện dùng trên xe có ghi 12V-15W. Mắc quạt vào hiệu điện thế 12V cho rằng hiệu suất của quạt là 85%, tính điện trở của quạt?
- Công suất tiêu thụ của quạt (P = 15W) gồm:
+ Công suất có ích (Công suất cơ học làm quạt quay):
\({P_{co\,hoc}} = 85\% .P\)
+ Công suất hao phí (Công suất tỏa nhiệt làm quạt nóng lên):
\({P_{toa\,nhiet}} = {I^2}R = P - {P_{co\,hoc}}\)
- Cường độ dòng điện qua quạt: \(I = \dfrac{{{P_{dm}}}}{{{U_{dm}}}} = \dfrac{{15}}{{12}} = 1,25A\)
- Công suất cơ học: \({P_{co\,hoc}} = 85\% .P = 85\% .15 = 12,75W\)
- Công suất tỏa nhiệt: \({P_{toa\,nhiet}} = P - {P_{co\,hoc}} = 15 - 12,75 = 2,25W\)
Điện trở của quạt: \(R = \dfrac{{{P_{toa\,nhiet}}}}{{{I^2}}} = \dfrac{{2,25}}{{1,{{25}^2}}} = 1,44\Omega \)

