I - LỰC - CÂN BẰNG LỰC
Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.
- Lực \(\overrightarrow F \) có:
+ Điểm đặt: nằm tại vật chịu tác dụng của lực
+ Phương, chiều: trùng với véctơ biểu diễn lực
+ Độ lớn lực: tỉ lệ với độ dài của véctơ biểu diễn lực

- Hai lực cân bằng là hai lực cùng tác dụng lên một vật, cùng giá, cùng độ lớn và ngược chiều.
- Đơn vị của lực là Niutơn (N).
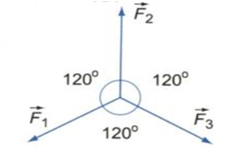
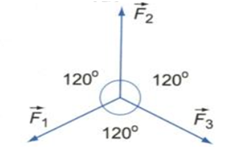
* Điều kiện cân bằng của một chất điểm
Hợp của tất cả các lực tác dụng lên nó bằng \(\overrightarrow 0 \)
\(\overrightarrow F = {\overrightarrow F _1} + {\overrightarrow F _2} + ... + {\overrightarrow F _n} = \overrightarrow 0 \)
II - TỔNG HỢP LỰC
1. Định nghĩa
Tổng hợp lực là thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt các lực ấy.
Lực thay thế này gọi là hợp lực.
2. Qui tắc hình bình hành.
Nếu hai lực đồng qui làm thành hai cạnh của một hình bình hành, thì đường chéo kể từ điểm đồng qui biểu diễn hợp lực của chúng.
\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
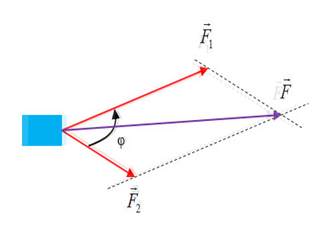
III - PHÂN TÍCH LỰC
Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
Các lực thay thế gọi là các lực thành phần.
IV - CÁC DẠNG BÀI TẬP
1. Tổng hợp lực
a. Tổng hợp lực của 2 lực thành phần: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
- Bước 1: Tịnh tiến các lực về cùng điểm đặt
- Bước 2: Nếu các lực không cùng phương thì sử dụng quy tắc hình bình hành để xác định véctơ tổng trên hình vẽ.
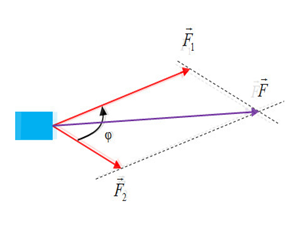
- Bước 3: Sử dụng biểu thức sau để xác định độ lớn lực tổng hợp
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\varphi } \)
* Các trường hợp đặc biệt:
- \({\overrightarrow F _1} \uparrow \uparrow {\overrightarrow F _2} \to F = {F_1} + {F_2}\)
- \({\overrightarrow F _1} \uparrow \downarrow {\overrightarrow F _2} \to F = \left| {{F_1} - {F_2}} \right|\)
- \({\overrightarrow F _1} \bot {\overrightarrow F _2} \to F = \sqrt {{F_1}^2 + {F_2}^2} \)
\(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)
b. Tổng hợp lực của 3 lực thành phần
* Cách 1:
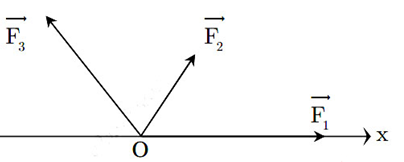
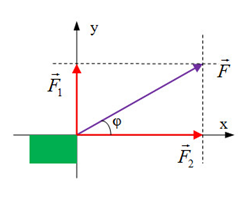
- Bước 1: Chọn hệ trục tọa độ Oxy
- Bước 2: Xác định các góc: \(\left( {{{\overrightarrow F }_1}{\rm{,Ox}}} \right) = {\alpha _1};\left( {{{\overrightarrow F }_2}{\rm{,Ox}}} \right) = {\alpha _2};...\)
- Bước 3: Tìm hình chiếu của các lực trên trục Ox, Oy:
\(\left\{ \begin{array}{l}{F_x} = {F_1}{\rm{cos}}{\alpha _1} + {F_2}{\rm{cos}}{\alpha _2} + ...\\{F_y} = {F_1}\sin {\alpha _1} + {F_2}\sin {\alpha _2} + ...\end{array} \right.\)
- Bước 3: Xác định độ lớn của hợp lực bởi công thức: \(F = \sqrt {F_x^2 + F_y^2} \) và \(\left( {\overrightarrow F {\rm{,Ox}}} \right) = \alpha \)
với \(\left[ \begin{array}{l}\tan \alpha = \frac{{{F_y}}}{{{F_x}}} \Leftrightarrow {F_x}{F_y} > 0\\\tan \alpha = - \frac{{{F_y}}}{{{F_x}}} \Leftrightarrow {F_x}{F_y} < 0\end{array} \right.\)
* Cách 2:
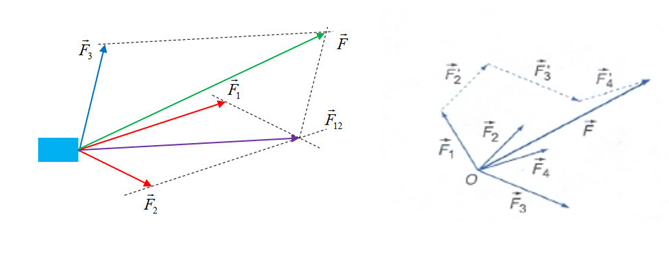
- Bước 1: Tổng hợp 2 lực 1
- Bước 2: Tổng hợp với lực thành phần còn lại
Sử dụng quy hình bình hành hoặc quy tắc đa giác
2. Phân tích lực
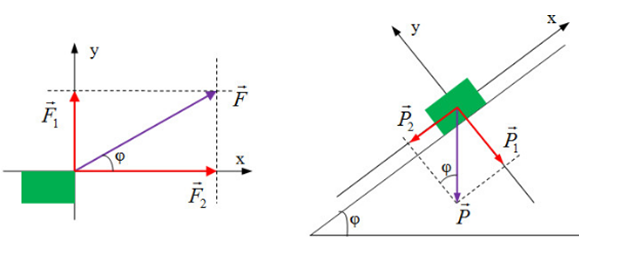
Căn cứ vào vị trí góc \(\varphi \) xác định được độ lớn của các lực thành phần:
\(\left\{ \begin{array}{l}{F_1} = F\sin \varphi \\{F_2} = Fc{\rm{os}}\varphi \end{array} \right.\) ; \(\left\{ \begin{array}{l}{P_1} = Pc{\rm{os}}\varphi \\{P_2} = P\sin \varphi \end{array} \right.\)