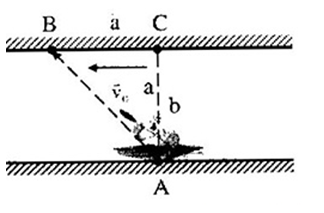
I - TÍNH TƯƠNG ĐỐI CỦA CHUYỂN ĐỘNG
1. Tính tương đối của quỹ đạo
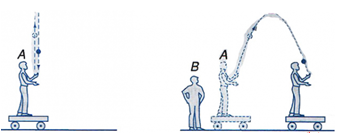
Quỹ đạo của chuyển động có tính tương đối, quỹ đạo trong các hệ quy chiếu khác nhau là khác nhau.
2. Tính tương đối của vận tốc.
Vận tốc của chuyển động có tính tương đối, vận tốc trong các hệ quy chiếu khác nhau là khác nhau.
II - CÔNG THỨC CỘNG VẬN TỐC
1. Hệ qui chiếu đứng yên và hệ qui chiếu chuyển động
- Hệ qui chiếu gắn với vật đứng yên gọi là hệ qui chiếu đứng yên.
- Hệ qui chiếu gắn với vật vật chuyển động gọi là hệ qui chiếu chuyển động.
2. Công thức cộng vận tốc.
\(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Trong đó:
+ Số 1: gắn với vật cần tính vận tốc
+ Số 2: gắn với hệ quy chiếu là các vật chuyển động
+ Số 3: gắn với hệ quy chiếu là các vật đứng yên
+ \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối
+ \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên gọi là vận tốc tuyệt đối.
- Độ lớn của vận tốc tuyệt đối:
\({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2 + 2{v_{12}}{v_{23}}{\rm{cos}}\alpha } \) với \(\alpha = \left( {\overrightarrow {{v_{12}}} ,\overrightarrow {{v_{23}}} } \right)\)
- Các trường hợp đặc biệt:
- \(\overrightarrow {{v_{12}}} \uparrow \uparrow \overrightarrow {{v_{23}}} \to {v_{13}} = v{}_{12} + {v_{23}}\)
- \(\overrightarrow {{v_{12}}} \uparrow \downarrow \overrightarrow {{v_{23}}} \to {v_{13}} = \left| {v{}_{12} - {v_{23}}} \right|\)
- \(\overrightarrow {{v_{12}}} \bot \overrightarrow {{v_{23}}} \to {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} \)