1. DẠNG 1: TÍNH THỜI GIAN - QUÃNG ĐƯỜNG - VẬN TỐC. QUÃNG ĐƯỜNG VẬT ĐI ĐƯỢC TRONG ΔT GIÂY THỨ N. THỜI GIAN VẬT ĐI QUA M THỨ N
Phương pháp :
- Vẽ hình - Đánh dấu các vị trí khảo sát - ghi các đại lượng động học
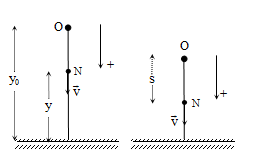
- Chọn HQC :
+ Gốc tọa độ O tại vị trí đầu.
+ Trục Oy thẳng đứng, chiều (+) trên xuống.
+ Gốc thời gian t = 0 lúc bắt đầu rơi.
- Áp dụng các công thức:
\(\left\{ \begin{array}{l}s = \frac{1}{2}g{t^2}\\v = gt\\{v^2} = 2g{\rm{s}}\end{array} \right.\) và \(\Delta s = {s_n} - {s_{\left( {n - 1} \right)}} = \frac{1}{2}gt_n^2 - \frac{1}{2}g{\left( {{t_n} - 1} \right)^2}\)
2. DẠNG 2: LIÊN HỆ GIỮA QUÃNG ĐƯỜNG, THỜI GIAN, VẬN TỐC CỦA HAI VẬT RƠI TỰ DO
Phương pháp :
- Vẽ hình - Đánh dấu các vị trí khảo sát của 2 vật - ghi các đại lượng động học.
- Chọn HQC :
+ Gốc tọa độ O tại vị trí đầu.
+ Trục Oy thẳng đứng, chiều (+) trên xuống.
+ Gốc thời gian t = 0 lúc vật bắt đầu rơi.
Nếu gốc thời gian không trùng lúc vật bắt đầu rơi thì \({t_0} \ne 0\)
- Áp dụng các công thức cho 2 vật:
\(s = \frac{1}{2}g{t^2}{\rm{; }}v = gt;{\rm{ }}{v^2} = 2g{\rm{s; }}y = {y_0} + \frac{1}{2}g{t^2}\)
3. DẠNG 3: CHUYỂN ĐỘNG CỦA VẬT ĐƯỢC NÉM THẲNG ĐỨNG HƯỚNG XUỐNG
Phương pháp :
- Chuyển động có :
+ Gia tốc : \(\vec a\) = \(\vec g\)
+ Vận tốc đầu : \({\vec v_0}\)cùng phương với \(\vec a\)
+ Phương trình : y = \(\frac{1}{2}\) gt2 + v0t+y0 (Chiều dương hướng xuống)
- Vẽ hình
- Đánh dấu các vị trí khảo sát của 2 vật - ghi các đại lượng động học.
- Chọn HQC :
+ Gốc tọa độ O tại vị trí đầu.
+ Trục Oy thẳng đứng, chiều (+) trên xuống.
+ Gốc thời gian t = 0 lúc vật bắt đầu ném.
Nếu gốc thời gian không trùng lúc vật bắt đầu rơi thì \({t_0} \ne 0\)
- Áp dụng các công thức cho 2 vật:
\(\begin{array}{l}s{\rm{ }} = \frac{1}{2}g{t^2} + {v_0}t\\v{\rm{ }} = {\rm{ }}gt{\rm{ }} + {v_0}t\\{v^2}-{v_0}^2 = {\rm{ }}2gs\\y = {y_0} + \frac{1}{2}g{t^2} + {v_0}t\end{array}\)
