Câu hỏi:
2 năm trước
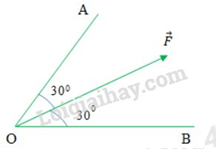
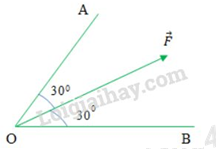
Phân tích lực \(\overrightarrow F \) thành lực \(\overrightarrow {{F_1}} \) và vecto lực \(\overrightarrow {{F_2}} \) theo hai phương OA và OB (hình 9 vẽ). Giá trị nào sau đây là độ lớn của hai lực thành phần?
Trả lời bởi giáo viên
Đáp án đúng: d
Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto \(\overrightarrow F \) lần lượt vẽ các đoạn thẳng song song với OA và OB ta đượcr \(\overrightarrow {{F_1}} \) trên OA và \(\overrightarrow {{F_2}} \) trên OB sao cho: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
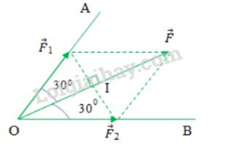
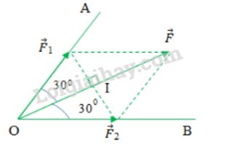
Ta có hình bình hành\(O{F_1}F{F_2}\) có đường chéo OF là đường phân giác của góc O nên \(O{F_1}F{F_2}\) là hình thoi
Tam giác F1OI vuông tại I có:
\(\begin{array}{l}\cos 30 = \dfrac{{OI}}{{O{F_1}}} \Rightarrow O{F_1} = \dfrac{{OI}}{{\cos 30}} = \dfrac{{\dfrac{{OF}}{2}}}{{\cos 30}} = 0,58.OF\\ \Rightarrow {F_1} = {F_2} = 0,58F\end{array}\)
Hướng dẫn giải:
Sử dụng quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng.
Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
