Câu hỏi:
2 năm trước
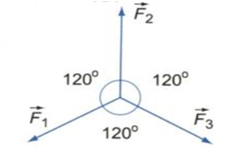
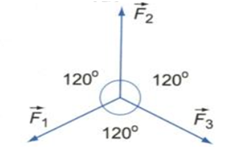
Cho ba lực đồng quy cùng nằm trong một mặt phẳng, có độ lớn bằng nhau và từng đôi một làm thành góc 1200 (hình vẽ). Tìm hợp lực của chúng.
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(\overrightarrow {{F_{123}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {{F_{12}}} + \overrightarrow {{F_3}} \)
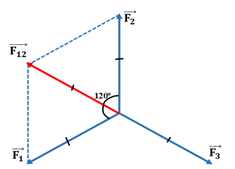
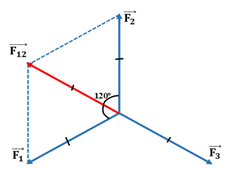
Vì \(\left\{ \begin{array}{l}{F_1} = {F_2}\\\left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right) = {120^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{F_{12}} = {F_1} = {F_2}\\\left( {\overrightarrow {{F_{12}}} ;\overrightarrow {{F_2}} } \right) = {60^0}\end{array} \right.\)
Do vậy \(\left\{ \begin{array}{l}\overrightarrow {{F_{12}}} \,\, \uparrow \downarrow \,\overrightarrow {{F_3}} \\{F_{12}} = {F_3}\end{array} \right. \Rightarrow \overrightarrow {{F_{123}}} = \overrightarrow {{F_{12}}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Hướng dẫn giải:
Sử dụng quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng.
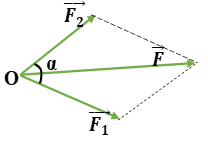
Biểu thức: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \)
