I. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
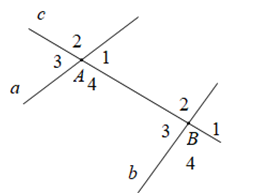
+ Hai cặp góc so le trong
\({\widehat A_4}\) và \({\widehat B_2}\); \({\widehat A_1}\) và \({\widehat B_3}\)
+ Bốn cặp góc đồng vị
\({\widehat A_2}\) và \({\widehat B_2}\); \({\widehat A_3}\) và \({\widehat B_3}\); \({\widehat A_4}\) và \({\widehat B_4}\); \({\widehat A_1}\) và \({\widehat B_1}\)
+ Hai cặp góc trong cùng phía
\({\widehat A_1}\) và \({\widehat B_2}\); \({\widehat A_4}\) và \({\widehat B_3}\)
II. Dấu hiệu nhận biết hai đường thẳng song song
Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
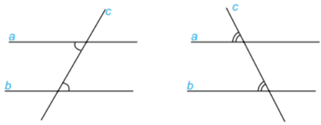
Chú ý: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
III. Tiên đề Euclid về đường thẳng song song
Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
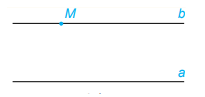
Chú ý: Nếu một đường thẳng cắt 1 trong 2 đường thẳng song song thì nó cũng cắt đường thẳng còn lại.
IV. Tính chất 2 đường thẳng song song
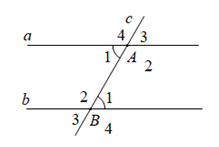
Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bù nhau
Ví dụ: \({\widehat A_1} = {\widehat B_1} \Rightarrow \left\{ \begin{array}{l}{\widehat A_2} = {\widehat B_2}\\{\widehat A_3} = {\widehat B_1}\\{\widehat A_2} + {\widehat B_1} = {180^0}\end{array} \right.\)
Chú ý:
+ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
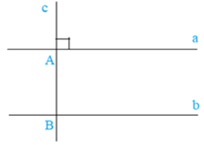
Nếu c ⊥ a, a // b thì c ⊥ b
+ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

Nếu \(a\parallel b;b\parallel c\) thì \(a\parallel c\).

