I. Khái niệm số thực và trục số thực
Số hữu tỉ và số vô tỉ được gọi chung là số thực. Kí hiệu: \(\mathbb{R}\)

Với $a,b$ là hai số thực dương, nếu \(a > b\) thì \(\sqrt a {\rm{\;}} > \sqrt b .\)
Ta có \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R};{\mkern 1mu} I \subset \mathbb{R}\).
Ví dụ: \(0,25 \in \mathbb{R}; - 3 \in \mathbb{R};...\)
Trục số thực
+ Mỗi số thực được biểu diễn bởi một điểm trên trục số.
+ Mỗi điểm trên trục số biểu diễn một số thực.

Chú ý: Các số thực lấp đầy trục số.
II. Thứ tự trong tập hợp các số thực
So sánh 2 số thực:
Các số thực đều viết được dưới dạng số thập phân (hữu hạn hay vô hạn). Ta có thể so sánh 2 số thực tương tự như so sánh số thập phân.
Ví dụ:
0,322 …< 0,324…nên 0,3(2) < 0,324…
- Với 2 số thực bất kì, ta luôn có hoặc a = b hoặc a > b hoặc a < b
- Nếu a < b ; b < c thì a < c (Tính chất bắc cầu)
- Nếu a < b thì điểm a nằm trước điểm b trên trục số
Chú ý: Nếu 0 < a < b thì \(\sqrt a < \sqrt b \)
Ví dụ: Vì 3 < 4 nên \(\sqrt 3 < \sqrt 4 = 2\)
III. Số đối của một số thực
Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này là số đối của số kia
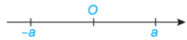
+ Số đối của số thực a là –a. Ta có: $a + (-a) = 0$
+ Số đối của số 0 là 0
Ví dụ: Số đối của \( - \sqrt 8 \) là \(\sqrt 8 \)
Nếu a > b thì $–a < -b$
IV. Giá trị tuyệt đối của một số thực
Khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là |a|
Nhận xét:
+ Hai số đối nhau thì có giá trị tuyệt đối bằng nhau
+ Giá trị tuyệt đối của 0 là 0
+ Giá trị tuyệt đối của một số dương là chính nó
+ Giá trị tuyệt đối của một số âm là số đối của nó
+ Giá trị tuyệt đối của một số thực luôn không âm.
Ví dụ:
$|2,3| = 2,3$
$|-2,3| = 2,3$
$|-2,3| = |2,3|$
Giả sử 2 điểm A và B lần lượt biểu diễn 2 số thực a và b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là $|a – b|$

