I. Chu vi và diện tích hình bình hành
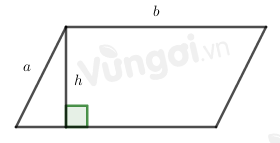
Chu vi hình bình hành : \(C = 2(a + b)\).
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
Chú ý: Khi tính chu vi và diện tích hình bình hành phải đưa các độ dài về cùng đơn vị đo.
Ví dụ:
Tính chu vi và diện tích của hình bình hành sau:
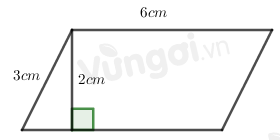
Hình bình hành trên có độ dài hai cạnh là 3 cm và 6 cm nên:
Chu vi hình bình hành trên là: \((3 + 6).2 = 18\) (cm)
Hình bình hành trên có độ dài đáy là 6 cm và đường cao là 2 cm nên:
Diện tích hình bình hành trên là: \(6.2 = 12\) (\(c{m^2}\)).
II. Chu vi và diện tích của hình thoi
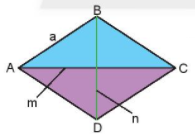
Chu vi hình thoi bằng độ dài cạnh nhân với bốn: \(C = 4a\)
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
Ví dụ 1:
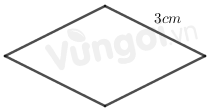
Chu vi hình thoi có cạnh bằng 3 cm là: \(4.3 = 12\,({m^2})\)
Ví dụ 2:
Hình thoi có độ dài hai đường chéo là 40 m và 20 m có diện tích là:
\(S = \frac{{40.20}}{2} = 400\,\,({m^2})\).

