I. Thế nào là chu vi và diện tích
1. Chu vi
Chu vi của một hình bất kì là độ dài phần đường thẳng bao quanh hình đó.
Ví dụ:
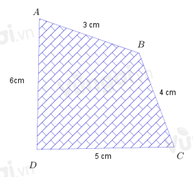
Chu vi của tứ giác ABCD bằng tổng độ dài bốn cạnh bao quanh nó, tức là:
AB+BC+CD+DA=3+4+5+6=18(cm).
Chú ý: Khi tính chu vi các hình thì độ dài các cạnh phải cùng đơn vị đo.
2. Diện tích
Diện tích của một hình là toàn bộ phần bên trong của hình đó.
Ví dụ:
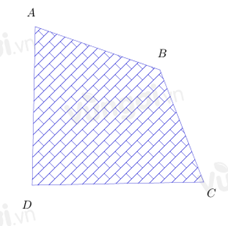
Diện tích của hình tứ giác trên là phần gạch xanh bên trong hình đó.
II. Chu vi và diện tích của hình vuông
Cho hình vuông có cạnh bằng a:
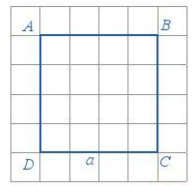
Chu vi hình vuông là: C=4a
Diện tích hình vuông là: S=a.a=a2.
Ví dụ 1:
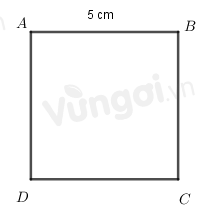
Chu vi hình vuông ABCD là: 4.5=20(cm2)
Diện tích hình vuông ABCD là: 52=25(cm2).
Ví dụ 2:
Một mảnh ruộng hình vuông có cạnh bằng 15m. Năng suất lúa là 0,9kg/m2. Tính diện tích mảnh ruộng và sản lượng thu hoạch được.
Diện tích mảnh ruộng hình vuông là: 152=225(m2).
Sản lượng thu hoạch được là: 225:0,9=312,5(kg).
III. Chu vi và diện tích hình chữ nhật
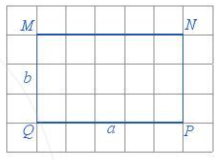
Chu vi của hình chữ nhật là: C=2(a+b);
Diện tích của hình chữ nhật là: S=a.b
Chú ý: Khi tính chu vi và diện tích thì chiều dài và chiều rộng phải cùng đơn vị đo.
Ví dụ 1:
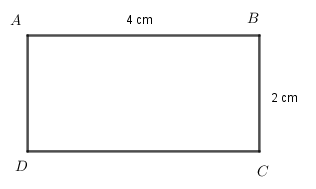
Chu vi hình chữ nhật ABCD là: 2.(4+2)=16(cm2).
Diện tích hình chữ nhật ABCD là: 4.2=8(cm2).
Ví dụ 2:
Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Loại gạch lát nền được sử dụng là gạch hình chữ nhật có chiều dài 20 cm, chiều rộng 50 cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?
Giải:
Diện tích căn phòng hình chữ nhật là: 8.6=48(m2)
Diện tích của một viên gạch là: 20.50=1000(cm2)=0,1(m2)
Số viên gạch bác Khôi cần dùng là: 48:0,1=480 (viên).
IV. Chu vi và diện tích của hình thang
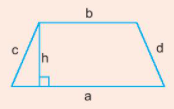
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
P=a+b+c+d
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
S=(a+b).h2
Chú ý: Cách làm trên vẫn áp dụng được để tính chu vi và diện tích hình thang cân.
Ví dụ 1:
Tính chu vi và diện tích hình thang sau:
Chu vi hình thang là: 2,5+3+4+7=16,5 (cm)
Diện tích hình thang là: (3+7).22=10 (cm2).
Ví dụ 2:
Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.
Diện tích hình thang cân là: (5+3,5).42=17 (cm2).

