Câu hỏi:
2 năm trước
Trong không gian với hệ trục tọa độ vuông góc \(Oxyz,\)cho mặt phẳng\(\left( P \right): - x + 2y + 2x - 3 = 0\), mặt cầu\(\left( S \right):{x^2} + {\rm{ }}{y^2} + {z^2} - 10x - 4y - 6z + 2 = 0\). Gọi \(\Delta \) là đường thẳng nằm trong mặt phẳng \(\left( P \right)\), đi qua \(A\left( {3;1;2} \right)\) và cắt \(\left( S \right)\) tại 2 điểm \(M,N\). Độ dài đoạn thẳng \(MN\) nhỏ nhất là
Trả lời bởi giáo viên
Đáp án đúng: b
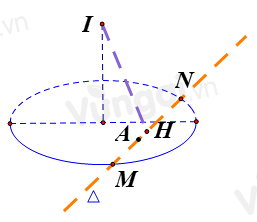
Mặt cầu (S) có:
\(I\left( {5;2;3} \right);R = \sqrt {{5^2} + {2^2} + {3^2} - 2} = 6\)
Mặt phẳng (P) có \(\overrightarrow {{n_{\left( P \right)}}} = \left( { - 1;2;2} \right)\)
\(d\left( {I,\left( P \right)} \right) = \dfrac{{\left| { - 5 + 2.2 + 2.3 - 3} \right|}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {2^2}} }} = \dfrac{2}{3} < R\)
=> Mặt phẳng (P) cắt mặt cầu (S)
\(IA = \sqrt {{{\left( {3 - 5} \right)}^2} + {{\left( {1 - 2} \right)}^2} + {{\left( {2 - 3} \right)}^2}} \)\( = \sqrt 6 < R\)
=> Điểm A nằm trong mặt cầu.
Gọi H là trung điểm của MN
Khi đó IH vuông góc với MN
\( \Rightarrow MN = 2HN\)\( = 2\sqrt {I{N^2} - I{H^2}} = 2\sqrt {36 - I{H^2}} \)
MN min\( \Leftrightarrow \)IH max
Tam giác IAH vuông tại H
=>\(IH \le IA\)
=> MN min ⬄ \(IH = IA = \sqrt 6 \)
\( \Rightarrow MN = 2\sqrt {36 - 6} = 2\sqrt {30} \)
Hướng dẫn giải:
Tìm tâm I, bán kính R của mặt cầu (S) và vtpt của mặt phẳng (P)
